Per funicula ad astra[41]

Являясь пионером освоения воздушного пространства, Дедал до сих пор не потерял интереса к проблемам аэронавтики и космонавтики. В настоящее время он размышляет над проблемами запуска искусственных спутников без использования ракет, которые, на его взгляд, несовершенны и неэкономичны. Дедал предлагает возвести на экваторе башню высотой 35700 км. Вершина такой башни, вращающейся вместе с Землей, движется с космической скоростью: достаточно поэтому поднять спутник наверх и оттолкнуть его. Если этот проект не будет принят, Дедал предлагает взамен более дешевый вариант: запустить на геостационарную орбиту высотой 40000 км спутник, к которому привязан трос. Другой конец троса закрепляется на экваторе, и спутник удерживает трос в натянутом состоянии. В дальнейшем по этому тросу можно было бы запускать небольшие спутники. К сожалению, из-за действия на запускаемый спутник кориолисовой силы трос будет отклоняться в сторону, противоположную направлению вращения Земли. Но Дедал надеется, что вскоре трос снова натянется и вернется в рабочее положение.

New Scientist, December 24, 1964

Вдохновленный отсутствием возражений по поводу его проекта «заякорить» на тросе геостационарный спутник, Дедал выдвигает еще более смелый проект. Он предлагает построить лифт на Луну. Для этого потребуется только достаточно мощная ракета, несущая трос в десять раз длиннее и с гарпуном на конце. При падении ракеты на Луну гарпун намертво закрепится в лунном грунте. Поскольку Луна всегда обращена к Земле одной стороной, на лунном конце троса никаких проблем не будет. Проблемы, как всегда, возникнут на Земле — из-за ее суточного вращения. Впрочем, трос можно закрепить на шарнире у Южного полюса. Если трос закрепить на экваторе, то он намотается на Землю и притянет Луну. Дедал, однако, опасается, что этот проект, несмотря на всю его привлекательность с точки зрения геофизиков и селенологов, вызовет возражения со стороны представителей Высокой Науки. Если же проект будет принят, то Дедал предлагает опустить Луну в Тихий океан, чтобы заодно проверить гипотезу, согласно которой этот океан образовался, когда Луна откололась от Земли.

New Scientist, October 16, 1965

1. Параметры геостационарного спутника

Период обращения спутника определяется уравнением Р² = 4πr²a³/GM, где Р — период обращения, G — универсальная гравитационная постоянная, равная 6,67×^-11 м³/кг•с², а — радиус орбиты, М — масса центрального тела (для Земли М = 5.97×10²⁴ кг). Поскольку Земля совершает один оборот за 24 ч (Р = 86400 с), в соответствии с этим уравнением получаем а = 42230 км. Спутник, находящийся на этом расстоянии от центра Земли, т. е. на высоте h = a - r⁰ = 42230 - 6370 = 35860 км над поверхностью Земли, будет «висеть» над одной и той же точкой экватора.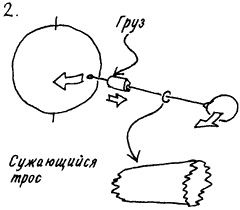

2. Привязной геостационарный спутник

Каждый участок троса должен выдерживать вес остальной части троса, расположенной ниже. Для этого трос должен утолщаться кверху приблизительно по экспоненциальному закону. Площадь сечения троса A_a вблизи спутника, находящегося на геостационарной орбите, связана с площадью сечения троса А₀ у поверхности Земли соотношением А_а ≈ А₀ exp(ρr₀g/Y), где ρ — плотность материала троса, g — ускорение силы тяжести у поверхности Земли, Y — модуль упругости материала троса, r₀ — радиус Земли.

3. Привязной спутник на шарнире Такой спутник может иметь любой период обраенияy (например, можно протянуть трос к Луне). Однако силы, действующие на ось, могут оказаться очень большими.

Комментарий Дедала

Эти две мои идейки появились на страницах журнала одними из первых. Они высказывались весьма неуверенно, ибо в ту пору редакция еще сомневалась, можно ли публиковать на страницах солидного журнала столь смелые предложения. Поэтому я был очень рад, когда основные положения обоих проектов были позднее повторены Дж. Д. Айзексом, А. Вайном, Г. Брэднером и Дж. Баккусом в журнале Science (151, Febr. 11, 1966, p. 682). Цитирую:

Помимо способности удерживаться в натянутом состоянии трос, закрепленный на экваторе вращающейся планеты или на естественном спутнике планеты (возможно, и на полюсе быстро вращающегося тела) и выходящий достаточно далеко за пределы орбиты стационарного спутника, будет обладать и другими интересными и полезными свойствами.

Массы, перемещаемые вдоль троса от поверхности центрального тела, будут запускаться в космическое пространство частично за счет энергии, отбираемой у вращающегося центрального тела.

Далее авторы рассчитывают прочность и сечеиие троса, указывают подходящие материалы для его изготовления и анализируют, на каких планетах и спутниках Солнечной системы этот проект легче всего реализовать.

Переписка с Артуром Кларком, в романе которого «Фонтаны рая» упоминается орбитальная башня высотой 35700 км, открыла мне, что эти мысли не так уж новы. Проект орбитальной башни впервые был предложен К. Э. Циолковским еще в 1895 г. Орбитальный трос был описан ленинградским инженером Ю. Арцутановым в «Комсомольской правде» от 31 июля 1960 г. Трос до Луны, по-видимому, придуман С. Голомбом в 1962 г. (Astronautics, 7–8, 1962, р. 26).

Артур Кларк сообщил мне: «…основная работа в этой области проводится Джеромом Пирсоном на базе ВВС США Райт-Паттерсон в штате Огайо. Его первая статья озаглавлена «Орбитальная башня»: установка для запуска космических аппаратов, использующая энергию вращения Земли» (Acta Astronautica, 2, 1975, p. 785). Пирсон думал, что эта идея целиком принадлежит ему, ибо библиографический поиск с помощью ЭВМ не выявил даже статью Айзекса!»

Наверное, следовало бы еще раз внимательно просмотреть и альбомы Леонардо да Винчи. Я утешаюсь тем, что фирма КОШМАР по крайней мере была одним из независимых авторов этих впечатляющих проектов.

Примечания:

4

К сожалению, проблема кпд теплового насоса до сих пор вызывает горячие споры (см., например, книгу [2], с. 268–275), кроме того, пережать капилляры простым трением руки, как предлагает Дедал, вряд ли возможно [3]. Инстинктивно потирая мерзнущие участки тела, едва ли можно пережать капилляр. — Прим. ред.

41

По канату — к звездам (лат.).