Усталость света

Загадочное «красное смещение» света, приходящего к нам от далеких галактик, обычно объясняется тем, что эти галактики удаляются от нас с огромной скоростью. Дедала, однако, больше привлекает гипотеза «усталости света», согласно которой свет по мере распространения постепенно теряет анергию, а следовательно, его частота понижается. Одно из затруднений состоит в том, что с релятивистской точки зрения при движении (в вакууме) со скоростью света время полностью «останавливается». Иначе говоря, перемещение фотонов на любое расстояние происходит мгновенно — как же в таком случае они могут «состариться» или «устать»? Однако даже в космическом пространстве свет движется не в абсолютном вакууме, а в среде, показатель преломления которой отличен от единицы, — соответственно скорость света в этой среде меньше скорости света в вакууме. Временные интервалы для фотонов сокращаются, но не до нуля, и свое путешествие в пространстве фотоны совершают не мгновенно. Правда, в космическом пространстве на 1 м³ объема приходится примерно лишь 100 атомов водорода и показатель преломления такой среды очень близок к единице (по расчетам Дедала, он равен 1 + 2,6×10^-28). Но и при этом фотон, проходящий путь в 10¹⁰ св. лет (расстояние, соответствующее уменьшению частоты в 2 раза), затратит на него примерно 2 ч «субъективного» времени, т. е. времени в системе отсчета движущегося фотона. Это дает Дедалу основание предположить, что за 2 ч фотон теряет половину своей энергии.

Для проверки этого замечательного вывода Дедал планирует следующий эксперимент. Известно, что показатель преломления воды намного выше, чем у межзвездного газа. Поэтому свет движется в воде значительно медленнее, и за 2 ч «субъективного» времени фотон пройдет в воде всего 2,7×10¹² м, а 1×10^-7 часть своей энергии свет потеряет на пути в 390 км. Соответствующий сдвиг частоты легко измерить лазерным интерферометром. Сейчас Дедал подыскивает подходящее место для прокладки прямолинейной трубы длиной в 400 км, заполненной водой. Наиболее подходящим местом для этого он считает равнину Налларбор в Австралии, где железнодорожный путь проложен строго по прямой на протяжении 500 км и трубу будет нетрудно установить параллельно рельсам. Если же этот смелый проект, направленный на решение ключевой проблемы современной космологии, не получит финансовой поддержки, Дедал намерен провести его под видом сооружения трансконтинентального водопровода.

New Scientist, March 9, 1972

Красное смещение света, приходящего от галактики, удаленной от нас на расстояние d м, равно -δv/v=Hd/v_изл, где Н — постоянная Хаббла, a v_изл — скорость распространения излучения, испытавшего красное смещение. Обычно красное смещение интерпретируется как доплеровский сдвиг частоты, возникающий из-за того, что галактика удаляется от нас с кажущейся скоростью v = Hd. Под скоростью распространения излучения v_изл обычно понимается скорость света в вакууме; однако поскольку межзвездный газ в действительности имеет коэффициент преломления, не равный 1, следовало бы принять v_изл = c/n, где n — показатель преломления среды. Считая эту зависимость линейной для небольших (по космическим масштабам) расстояний, мы можем принять d = δl; тогда -δv/v=nHδl/c.

Обозначив величину c/nH через L, получим -δv/v=δl/L. (1)

Если понимать это выражение как меру «усталости» света (т. е. считать, что при прохождении в среде расстояния δl частота света уменьшается на δv), то, проинтегрировав (1), мы получим выражение для уменьшения частоты на конечном пути l: v = v₀exp(-l/L). (2)

Здесь v₀ — исходная частота света, a v — его частота после прохождения пути l в преломляющей среде. Частота света уменьшается в е раз на пути l = L; L поэтому можно назвать «характеристическим космическим расстоянием», L_характ. Аналогично можно ввести характерный масштаб, на котором частота света уменьшается вдвое: L_1/2 = L_характln2 = 0,69c/nH. Поскольку n очень близко к 1, это значение хорошо согласуется с величиной L_1/2 = 0,6c/H, полученной из формулы для доплеровского сдвига с релятивистской поправкой. Какое время t_характ затрачивает фотон на прохождение характеристического расстояния L_характ? В межгалактической среде с показателем преломления n свет распространяется со скоростью v_изл=c/n, и искомое время для неподвижного наблюдателя будет равно t = L_характ/v_изл. Подставляя c/n вместо v_изл cn/H вместо L_характ, получаем t = 1/H. В системе отсчета, связанной с фотоном, происходит релятивистское сокращение времени в (1 - v²_изл/c²)^1/2 раз или (так как v_изл=c/n) в (1-1/n²)^1/2 раз. Поэтому «субъективное» время, за которое частота фотона уменьшается в е раз, равно τ = (1-1/n²/H)^1/2. (3)

Я считаю, что уменьшение частоты фотона, которое мы наблюдаем как красное смещение, вызвано его старением в собственной системе отсчета по экспоненциальному закону, который описывает, например, и радиоактивный распад. С этой точки зрения τ можно понимать как характеристическое время старения фотона в уравнении, аналогичном уравнению (2): v=v₀exp(-t/τ), где t — текущее время в системе отсчета, связанной с фотоном, a v₀ — исходная частота фотона.

В таком случае τ является характеристической константой для фотона, и, как следует из уравнения (3), мы можем определить ее через постоянную Хаббла и показатель преломления межгалактической среды n. Попытаемся это сделать.

Показатель преломления газовой среды довольно хорошо аппроксимируется выражением n = 1 + kN, где N — число атомов (молекул) на 1 м³, a k — некая постоянная, характеризующая данный газ. Подставив это выражение в (3), получим в первом приближении τ = (2kN/H)^1/2.

Для водорода при 0°C и давлении 1 атм N = 5,3×10²⁵ м^-3 и n =1,000138, откуда k = 0,000138/(5,3×10²⁵) = 2,6×10^-30 м³. В межзвездном газе содержится примерно 100 атомов водорода на 1 м³ объема, а постоянная Хаббла H≈2×10¹⁸ с^-1; тогда

Соответствующее «время полураспада» фотона составляет τ_1/2= τln2 = 7900 с, или около 2 ч. Жизнь фотона, оказывается, коротка!

Можно ли проверить эти выводы на опыте? Проведенные рассуждения относятся к любой преломляющей среде. Поэтому для любой среды мы можем определить средние значения «постоянной Хаббла» H_ср и «характеристического расстояния» L_cp по известному показателю преломления n_ср и полученному значению τ:

Для среды с высоким показателем преломления характеристическое расстояние L_cp будет невелико, поскольку скорость распространения света существенно ниже, чем в вакууме. Например, для воды (n = 1,33)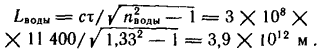

(Соответствующее расстояние L_1/2 для воды равно L_водыln2 = 2,7×10¹² м.)

Согласно (1), снижение частоты света на пути δl в воде равно

Тогда уменьшение частоты на одну десятимиллионную долю (такое изменение частоты нетрудно зарегистрировать современными методами) должно произойти на пути, равном δl = 10^-7×3,9×10¹² = 3,9×10⁵ м = 390 км.

Похоже, что подобный эксперимент вполне можно было бы поставить на практике.

Комментарий Дедала

С тех пор как в 1972 г. я проделал эти расчеты, техника волоконных световодов и методы точных измерений частоты шагнули далеко вперед и проведение предлагаемого эксперимента стало еще более реальным. Заметное красное смещение должно произойти, когда свет пройдет внутри световода расстояние всего лишь в несколько километров.