Глава 4: Логическая перспектива

Мы уже наблюдали свидетельство, позволяющее предположить, что атом — это эфирный вихрь, обладающий сферической симметрией и центральной осью, то есть, сферический тор. Эффект Бифилда-Брауна показывает, что великое решение загадки “полярности заряда” состоит в том, что эфирная энергия течет через электронные облака в ядро. Д-р Гинзбург произвел насколько простых и приемлемых подгонок уравнений относительности и разработал модель, совершенно объясняющую поведения материи, наблюдаемые Козыревым в лаборатории, когда, ускоряясь до скорости света, она теряла энергию и массу.

Знакомясь с обычными кристаллическими молекулами в виде тетраэдра, куба и октаэдра, и особенно с микрокластерами, икосаэдральными и додекадральными квазикристаллами и феноменом конденсатов Бозе-Эйнштейна, мы видим важность Платоновых Твердых Тел в квантовой сфере. Мы больше не можем отрицать существование этих сил, поскольку имеем неопровержимое физическое свидетельство. Также, новые находки раскрывают, что нам больше не нужно думать об атомах как об индивидуальных единицах, скорее о них следует думать как о гармонических эфирных вихрях, способных сливаться в бо льшие уровни единства и гармонии, такие как квазикристаллы. При наличии этой информации и с помощью работы Рода Джонсона, у нас есть решение всех “утерянных концов” головоломки.

В модели Джонсона мы видим следующее:

• “Твердых” частиц не существует, есть только группирования энергии.

• Каждое квантовое измерение можно геометрически объяснить как форму структурированных, пересекающихся энергетических полей.

• Атомы — это вращающиеся в противоположных направлениях энергетические формы в виде Платоновых Твердых Тел, а именно вращающиеся в противоположных направлениях октаэдр и тетраэдр. Причем каждая вибрационная/пульсирующая форма соответствует конкретной основной плотности эфира.

• Во всей Вселенной, все уровни плотности или измерения структурированы из двух первичных уровней эфира, непрерывно взаимодействующих между собой.

Растет число продвинутых теоретиков, склоняющихся к физике “сетки частиц”, основанной на теории Суперструн, в которой вся материя во Вселенной является элементом взаимосвязанной геометрической матрицы. Однако, поскольку традиционные ученые еще не визуализировали Платоновы Твердые Тела, загнездованные друг в друге, делящие общую ось и способные вращаться в противоположных направлениях, они утеряли картину квантовой реальности.

И вновь, в этой главе, излагая обзор модели Джонсона, мы попытаемся придерживаться простоты. Сначала мы расскажем о том, “что происходит” на квантовом уровне, а затем обсудим научное свидетельство, чтобы это доказать. Мы начинаем наш обзор основных принципов модели с заштрихованной карандашом иллюстрации переплетенного (звездного) тетраэдра, которую мы создали для того, чтобы ясно продемонстрировать, как он выглядит в трехмерном изображении. Важно, чтобы у нас был хороший визуальный образ этой структуры прежде, чем мы попытаемся представить вписанный в него октаэдр. На рисунке мы можем ясно видеть два тетраэдра, один с вершиной, направленной вверх, другой с вершиной, направленной вниз. Также, помните, что вся структура идеально вписывается в сферу.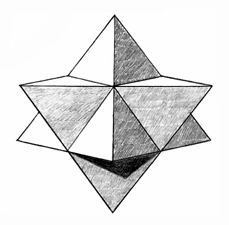

Рис. 4.1 Переплетенный (звездный) тетраэдр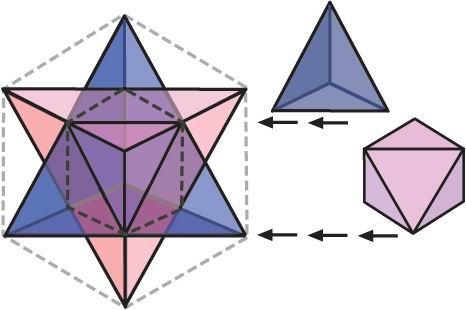

Рис. 4.2 Октаэдр (справа) и его расположение внутри переплетенного тетраэдра

Держа в уме эту структуру (рис. 4.1), рассмотрим следующие положения модели:

• На квантовом уровне тетраэдр и октаэдр вращаются в противоположных направлениях внутри друг друга.

• Оба они обладают сферической симметрией вокруг общего центра.

• Тетраэдр и октаэдр представляют два первичных уровня эфирной плотности, которые должны существовать во Вселенной. Мы обозначим их Э1 и Э2.

• Поле октаэдра совершенно размещается в центре поля тетраэдра, поэтому диаметр октаэдра меньше, что можно видеть на рис. 4.2

Рис. 4.2 демонстрирует октаэдр внутри переплетенного тетраэдра, который, в свою очередь, находится внутри куба. Сначала, попытка представить октаэдр как свободную добавку, способную вращаться в противоположном направлении внутри переплетенного тетраэдра, может оказаться неудачной. Конечно, в этой форме две геометрии полностью сбалансированы и совмещены. Однако самая важная часть физики Джонсона — увидеть, что октаэдр “отсоединен” и действует отдельно от поля тетраэдра посредством вращения в противоположном направлении. Существует всего восемь возможных “фазовых” положений, в которых две геометрии могут умещаться друг в друге прежде, чем снова достигнут гармонии, наблюдаемой выше. Чтобы обрести фазовое положение, две геометрии должны иметь какую-то степень прямого контакта друг с другом, либо ребро к ребру, либо вершина с вершиной. Графически это иллюстрируется на нижеприведенной “фазовой” схеме: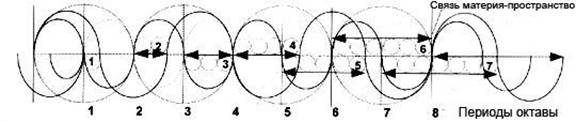

Рис. 4.3 Восемь “фазовых положений”, созданных вращением октаэдра и тетраэдра в противоположных направлениях

На схеме мы видим две основные волны: меньшая волна, которая укладывается в каждую из четырех главных окружностей, представляет собой вращение октаэдра, бо льшая волна, вне границ главной окружности, представляет собой вращение тетраэдра в противоположном направлении. Эта схема — самый легкий способ показать, как и где будут соединяться октаэдр и тетраэдр. Она основана на науке “фазовой физики”, впервые разработанной Кеннетом Г. Уилсоном как средство распределения крупно масштабных геометрических взаимосвязей, таких как волновые движения. Каждое из восьми “фазовых положений” представляет собой отдельный элемент, и это показано на следующем рисунке: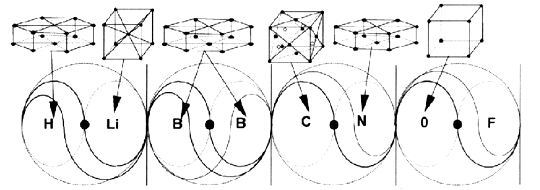

Рис. 4.4 Восемь “фазовых положений” и как они соотносятся с основными кристаллическими структурами, сформированными элементами

Итак, продолжим:

• И тетраэдр, и октаэдр пребывают под большим давлением: тетраэдр толкается по направлению к октаэдру, аналогично тому, как отрицательное электронное облако толкается по направлению к ядру.

• Давление может высвобождаться только тогда, когда узел или ребро одного твердого тела пересекает узел или ребро другого твердого тела, открывая проход для течения энергии.

Самый легкий способ визуализировать “проход” таков: вы вырежьте отверстие в кусочке картона, затем включите фен, установите наконечник прямо напротив картона, и скользите им по направлению к отверстию. Пока наконечник ни достигнет отверстия, воздуху некуда идти, и фен будет быстро перегреваться. Но как только наконечник достигнет отверстия, воздуху есть куда идти, и давление высвобождается. Внутри атома, посредством эффекта Бифилда-Брауна, давление в электронных облаках всегда стремится двигаться по направлению к ядру, и до тех пор, пока движущиеся в противоположных направлениях геометрии не соединятся, давление блокировано. В этом смысле, ребра и узлы в геометрических формах могут рассматриваться как “отверстия”, “втиснутые” в загнездованные сферические поля и позволяющие истечение втекающего давления.

Однако это решает лишь одну проблему “давления”. Также следует помнить про давление, создаваемое силами октаэдра и тетраэдра, вращающимися в противоположных направлениях. Именно эти геометрии формируют в “пузырьках поля” то, что теперь мы называем соответственно эфир 1 (Э1) и эфир 2 (Э2). Древние традиции часто называли Э1 и Э2 “положительной и отрицательной силой”. До тех пор пока в точке геометрического равновесия октавы не выстроится самое большое число “отверстий” между двумя геометриями, общее количество внешнего давления не может течь к центру. Поэтому, когда две формы “заперты” в периодах валентности, не находящихся в точке “октавы”, вращение Э1 и Э2 в противоположных направлениях сбалансировано не полностью, что создает дополнительное давление и несимметричность. Тогда, Э1 и Э2 будут оставаться “застрявшими” в несбалансированном положении, если не возмущаются внешней энергией.

Именно таким образом “застревает” большинство элементов Периодической Таблицы Элементов Д. Менделеева, следовательно, они не стабильны. Поэтому, все естественно возникшие и не радиоактивные элементы организованы в таблице слева направо в группах по восемь. Они движутся из положения нестабильности и несимметричности (слева) в положение большей кристаллической симметрии и геометрического равновесия (вправо). В модели Джонсона, геометрии вновь обретают совершенное равновесие только тогда, когда мы двигаемся к Октаве или восьмому фазовому положению вращения в противоположных направлениях.

Это можно визуализировать с помощью идеи сидения на узком стуле. Очевидно, что самое удобное сидячее положение будет в том случае, если тело центрировано посередине. А теперь представьте, что вы пытаетесь сидеть на стуле в восьми разных положениях. Начните с того, что стула касается только маленькая часть одной из ваших ног. Каждое положение будет неудобным, и вы не обретете полного равновесия до тех пор, пока полностью не центрируетесь на стуле. Отсюда, атомы и молекулы, не пребывающие в состоянии равновесия, считаются “нестабильными” и будут легко связываться с другими нестабильными атомами и молекулами, удерживающими энергию, недостающую для восстановления равновесия.

Первая форма таких связей известна как ковалентная связь. Такое название используется потому, что считалось, что “валентные связи” электронных облаков “делятся” между данными атомами. Как мы уже говорили, как таковых “электронов” не существует, и такую связь формирует именно завершение геометрической симметрии между Э1 и Э2 (загнездованными тетраэдром и октаэдром). В модели Джонсона, все элементы представляют собой смеси Э1 и Э2 в разных пропорциях, то есть загнездованные тетраэдр и октаэдр, запертые в различных положениях относительно друг друга. Самый простой пример: один атом кислорода будет естественно притягиваться к двум атомам водорода и смешиваться в молекулу воды или H2 O. Не удивительно, что молекула воды принимает форму тетраэдра.

Другой вариант основных связей в химии известен как “ионные связи”. В этом случае, связи создаются разницей в полярности заряда, когда отрицательное притягивает положительное. Когда элемент обладает несбалансированным зарядом, он известен как ион, отсюда и термин ионная связь. Самым простым примером был бы хлористый натрий или соль, который может записываться как Na + Cl. Он формирует либо куб, либо октаэдр. Именно разница давлений между положительными и отрицательными ионами притягивает их друг к другу. В молекуле соли атомы хлора имеют ширину 1,81 ангстрема, почти вдвое больше, чем атомы натрия — 0,97 ангстрема.

Также, ионная связь может возникать, когда отдельные атомы конкретного элемента притягиваются друг к другу и связываются вместе по двое, создавая симметрию. Самый очевидный пример — молекула кислорода, О2. Единственный способ, посредством которого древние (ал)химики могли находить исходные элементы, такие как единичный атом кислорода, — это разложение основных химических соединений посредством горения, замораживания, смешивания с кислотами и основаниями и так далее.

Итак, возвращаясь к основному положению: у нас есть восемь основных положений или фаз, в которых могут быть расположены тетраэдр и октаэдр. Однако любой проницательный читатель уже заметил, что восьми основных геометрических положений явно недостаточно для формирования всей Периодической Таблицы; чтобы создать полный набор природных элементов, должны работать еще какие-то дополнительный свойства.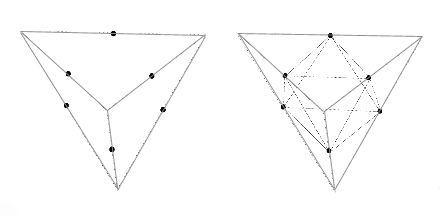

Рис. 4.5 Частотное расширение тетраэдра в октаэдр

Вот ключ:

Обе геометрические формы способны расширяться и сжиматься из своих центров.

Это называется изменением частоты.

Меняя частоту, они формируют разные виды геометрических твердых тел.

Эти твердые тела — не Платоновы, могут быть и другие формы, такие как твердые тела Архимеда, но все они связаны посредством “родительских” тетраэдра и октаэдра.

Как видно на рис. 4.5, сжатие геометрической формы — это деление всех ребер на две или более равных частей, а затем соединение полученных точек. Если мы делим каждое ребро на половины, это называется “второчастотное” деление, если мы делим каждое ребро на три равные части, такое деление называется “третье-частотное” деление. Начиная с тетраэдра, Бакминстер Фуллер продемонстрировал, что посредством процесса расширения или сжатия можно получить всего десять разных частот (геометрических форм), и это центральный аспект находок Джонсона. Например, известно, что “мощная” сила в атомном ядре в десять раз сильнее “слабой” силы в электронных облаках! Обычно это записывается как квадратный корень из 100, равный 10. Никакого иного правдоподобного объяснения этой аномалии не найдено. То есть, ядро представляет собой точку самой “свернутой” геометрии на самом высоком частотном уровне сжатия.

Итак, все, что нужно сделать, — это объединить восемь основных фаз вращающейся в противоположных направлениях геометрии с различными частотами геометрии, возникающей в результате расширения или сжатия. Таким способом можно получить всю Периодическую Таблицу. Кроме того, вы можете предсказать, будет ли элемент твердым, жидкостью или газом, а также, каковы будут его точки замерзания, плавления или испарения. Джонсон направляет заинтересованных мыслителей к работе Джеймса Картера, которому удалось получить всю Периодическую Таблицу посредством схем спиралевидного движения, которые он назвал “круглонами”. И самое интересное: “круглоны” Картера являются сферическими торами! Представляется, что Картер не знал, что спиралевидные, волнообразные, циклические “вращения во вращениях” и были тем, что он изображал между круглонами для демонстрации различных элементов, то есть, они существуют посредством “абсолютного движения”. В целях более полного описания, мы приглашаем читателя, ознакомиться с нашей детальной статьей и/или вебсайтом Картера. В целях упрощения, мы приведем некоторые наиболее очевидные признаки из квантовой физики, указывающие на работу Платоновых геометрий.

Большинство людей уже знает: считается, что тепловое излучение и свет создаются очень простой вещью — движением вспышек электромагнитной энергии, известных как “фотоны”. Однако до 1900 года считалось, что свет и тепло движутся не в форме дискретных (прерывистых) единиц “фотонов”, а гладко, плавно и неразрывно. Физик Макс Планк первым открыл, что на самом крошечном уровне свет и тепло движутся “пульсациями” или “пакетами” энергии, величиной 10-32 см. По сравнению с таким размером атомное ядро было бы величиной с планету! Интересно следующее: чем быстрее колебание, тем больше пакеты, и, соответственно, чем медленнее колебание, тем меньше пакеты. Планк открыл, что отношение между скоростью колебания и размером пакета всегда остается постоянным, не зависимо от того, как вы их измеряете. Постоянное отношение между скоростью колебания и размером пакета известно как Закон Распределения Вейна. Планк обнаружил единственное число, выражающее это отношение. Сейчас оно известно как “Постоянная Планка”.

Недавно опубликованная статья Каролин Хартман (декабрьский 2001 года выпуск журнала Наука и техника 21-го века) посвящена исключительно находкам Макса Планка. Она раскрывает, что головоломка, созданная его открытиями, остается нерешенной:

“Сегодня, в целях более глубокого проникновения в структуру атома, наш долг — продолжать исследования таких ученых как Кюри, Лиза Мейтнер и Отто Ган. Но фундаментальные вопросы: что вызывает движение электронов, подчиняется ли это движение определенным геометрическим законам, и почему одни элементы более устойчивы, чем другие, все еще не имеют ответов и ожидают новых передовых гипотез и идей”.

В этой книге мы уже можем видеть ответ на вопрос Хартман. Как мы уже сказали, открытия Планка совершались в результате изучения теплового излучения. Вводный параграф в статье Каролин Хартман — совершенное описание его достижений:

“Сто лет назад, 14 декабря 1900 года, физик Макс Планк (1858–1947) объявил (в речи перед Обществом Кайзера Вильгельма в Берлине) о своем открытии новой формулы излучения, которая могла бы описывать все закономерности, наблюдаемые при нагревании материи, когда она начинает испускать тепло разных цветов. Причем его новая формула основывалась на одном важном допущении: энергия излучения не непрерывна, излучение происходит только пакетами определенного размера. Трудность в том, как сделать стоящее за “формулой” допущение физически понятным. Что имеется в виду под “энергетическими пакетами”, которые даже не постоянны, а меняются пропорционально частоте колебания (Закон Распределения Вейна)?”

Немного позже, Хартман продолжает:

“(Планк) знал: когда бы вы ни наталкивались на, по-видимому, неразрешимую проблему в Природе, в ее основе должны лежать более сложные закономерности; иными словами, должна существовать иная “геометрия Вселенной”, чем считалось раньше. Например, Планк всегда настаивал на том, что надежность уравнений Максвелла следует пересмотреть, потому что физика достигла такой стадии своего развития, при которой так называемые “физические законы” больше не универсальны”.

Зерно работы Планка может быть выражено простым уравнением, описывающим, как излучающая материя высвобождает энергию в “пакетах” или вспышках. Это уравнение Е = hv, где Е — это конечная измеряемая энергия, v — частота вибрации излучения, высвобождающего энергию, и h — известна как “Константа Планка”, регулирующая “поток” между v и E.

Константа Планка равна 6,626. Это отвлеченное выражение, поскольку выражает чистое отношение между двумя величинами и не нуждается в присвоении любой конкретной категории измерения, иной, чем эта. Планк открыл эту константу не чудом, скорее он скрупулезно вывел ее посредством изучения многих разных видов теплового излучения.

Это первая главная тайна, которую проясняет Джонсон в своем исследовании. Он напоминает: для измерения константы Планка используется декартова (прямоугольная) система координат. Эта система названа по имени ее создателя Рене Декарта и означает, что для измерения трехмерного пространства используются кубы. Она стала настолько привычной, что большинство ученых даже не считают ее чем-то необычным, просто длина, ширина и высота. В экспериментах, таких как эксперименты Планка, для измерения энергии, движущейся через определенную область пространства, используется маленький куб. В измерительной системе Планка, в целях простоты, этому кубу был естественно присвоен объем “единицы” (1). Однако когда Планк писал свою константу, он не хотел иметь дело с десятичным числом, и поэтому сдвинул объем куба до 10. Это сделало константу равной 6,626 вместо 0,6626. По-настоящему важным было отношение между чем-то, находящимся внутри куба (6,626), и самим кубом (10). Не имеет значения, присваиваете ли вы кубу объем единицы, десяти или любого другого числа, поскольку отношение всегда остается постоянным. Как мы говорили, Планк разгадал постоянную природу этого отношения только посредством тщательных многолетних экспериментов.

Помните, что в зависимости от размера высвобождаемого пакета, вам понадобиться измерять его разного размера кубом. И все же, что бы ни находилось внутри куба, оно всегда будет иметь 6,626 единиц объема куба, если объем самого куба 10 единиц, независимо от вовлеченных в процесс размеров. Прямо сейчас следует отметить: величина 6,626 очень близка к 6,666, что является точно 2/3 от 10. Поэтому, следовало бы спросить: “А что такого важного в 2/3?”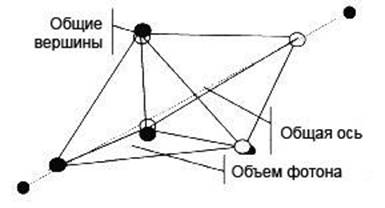

Рис. 4.6 Два тетраэдра, соединенные общей гранью для формирования “фотона”, измеренного с помощью Постоянной Планка

Основываясь на простых измеряемых геометрических принципах, объясненных Фуллером и другими, мы знаем: если совершенно разместить тетраэдр внутри сферы, он будет заполнять ровно одну треть ее общего объема. На самом деле, фотон состоит из двух соединенных вместе тетраэдров, что мы видим на рис. 4.6. Затем они вместе проходят через куб, который достаточно велик только для того, чтобы вмещать один из октаэдров за раз. Общий объем (энергии), движущейся через куб, будет ровно две трети (6,666) общего объема куба, которому Планк присвоил число 10. Бакминстер Фуллер первым открыл, что фотон составлен двумя тетраэдрами. Он объявил об этом миру в 1969 году на Planet Planning, после чего об этом было полностью забыто.

Небольшая разница 0,040 между “чистым” 6,666 или отношением 2/3 и константой Планка 6,626 создается удельной емкостью вакуума, который поглощает некоторое количество энергии. “Удельную емкость вакуума” можно точно вычислить с помощью того, что известно как уравнение Кулона. Выражаясь более простыми терминами, эфирная энергия “физического вакуума” будет поглощать небольшое количество любой проходящей через него энергии. Это значит, что физический авкуум будет “позволять” проходить через него чуть меньше энергии, чем высвобождено изначально. Поэтому, как только мы учитываем уравнение Кулона, числа работают совершенно. Более того, если мы измеряем пространство, используя тетраэдральные координаты вместо кубических, необходимость в уравнении Планка Е = hv отпадает, ибо в этом случае энергия будет измеряться одинаково на обеих сторонах уравнения, то есть Е (энергия) будет равна v (частоте), и “константа” между ними не нужна.

“Пульсации” энергии, продемонстрированные константой Планка, известны квантовым физикам как “фотоны”. Обычно мы думаем о “фотонах” как о носителях света, но это лишь одна из их функций. Более важно следующее: когда атомы поглощают или высвобождают энергию, она передается в форме “фотонов”. Исследователи, такие как д-р Мило Вольф, напоминают: единственное, что мы точно знаем о термине “фотон”, - он является импульсом, проходящим через эфир/энергетическое поле нулевой точки. Сейчас можно видеть, что эта информация содержит геометрический компонент, что позволяет предполагать, что атомы должны обладать такой же геометрией.

Еще одной недавно открытой аномалией, демонстрирующей присутствие геометрии на квантовом уровне, является Теорема Неравномерности Белла. В данном случае два фотона высвобождаются в противоположных направлениях. Каждый фотон испускается из отдельной возбужденной атомной структуры. Две атомные структуры состоят из идентичных атомов, и обе распадаются с одинаковой скоростью. Это позволяет двум “спаренным” фотонам с одинаковыми энергетическими качествами одновременно высвобождаться в противоположных направлениях. Затем оба фотона проходят через поляризационные фильтры, такие как зеркала, что теоретически должно изменить направление их движения. Если одно зеркало расположено под углом в 45°, а другое под углом в 30°, было бы естественно ожидать, что угловые повороты фотонов будут разными.

Однако когда выполнялся этот эксперимент, не смотря на разницу в углах зеркал, фотоны одновременно совершили одинаковый угловой поворот!

Степень точности эксперимента ошеломляет, что описывается на страницах 142–143 книги д-ра Мило Вольфа:

“В самом последнем эксперименте Аспекта, чтобы полностью устранить любую возможность местных влияний одного детектора на другой, Дэлибард и Роджер использовали акустико-оптические переключатели на частоте 50 МГ, сдвигающие наборы поляризаторов во время полета фотонов…

Теорема Белла и результаты эксперимента свидетельствуют о том, что части Вселенной связаны на каком-то внутреннем уровне (то есть, не очевидном для нас), и эти связи фундаментальны (квантовая теория фундаментальна). Как мы можем их понять? И хотя проблема анализировалась очень глубоко (Вилер и Зурек, 1983; д’Эспанья, 1983; Герберт, 1985; Стап, 1982; Бом и Хили, 1984; Пэйджелс, 1982; и другие), решение не найдено. Авторы склонны согласиться со следующим описанием нелокальных связей:

1. Они связывают события в отдельных местах без известных полей или материи.

2. Они не ослабляются с расстоянием; будь то миллион километров или сантиметр.

3. Представляется, что они распространяются быстрее, чем скорость света.

Бесспорно, в рамках науки это весьма озадачивающий феномен.

Теорема Белла гласит: энергетически спаренные “фотоны” реально удерживаются вместе единственной геометрической силой, а именно тетраэдром, продолжающим расширяться (становиться больше) при разделении фотонов. Поскольку геометрия между ними расширяется, фотоны будут продолжать сохранять одинаковое угловое фазовое положение относительно друг друга.

Поскольку Эйнштейн определил, что материя состоит из электромагнитной энергии, следующий пункт нашего исследования — сама электромагнитная волна. Как знает большинство людей, электромагнитная волна имеет два компонента — электростатическую волну и магнитную волну, которые движутся вместе. Чтобы визуализировать, происходящее, Джонсон просит взять два карандаша одинаковой длины и установить их перпендикулярно друг другу; причем расстояние между ними должно равняться длине карандаша.

Теперь мы можем соединить каждый конец верхнего карандаша с каждым концом нижнего карандаша. Сделав это, мы получим четырехсторонний объект, составленный равносторонними треугольниками между двумя карандашами, то есть тетраэдр.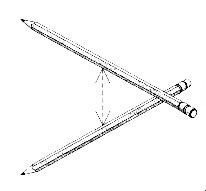

Рис. 4.7 Два карандаша, расположенные на одинаковом расстоянии под углом в 90°

Тот же самый процесс можно проделать с электромагнитной волной, приняв общую высоту электростатической или магнитной волны (которые обладают одинаковой высотой или амплитудой) за основную длину, как у карандашей на рис. 4.7. На рис. 4.8 можно видеть, что электромагнитная волна на самом деле копирует “скрытый” (потенциальный) тетраэдр, если мы соединим линии, используя тот же самый процесс: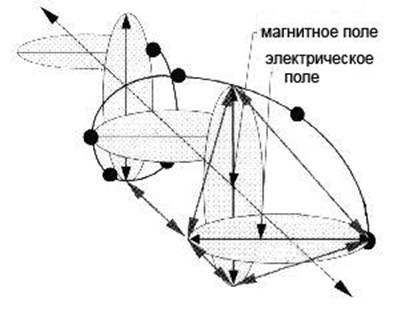

Рис. 4.8 Скрытые тетраэдральные отношения в электромагнитной волне

Здесь важно упомянуть: эта тайна неоднократно открывалась разными мыслителями, только для того, чтобы снова оказаться забытой наукой. Работа Тома Бирдена убедительно показала, что Джеймс Клерк Максвелл знал об этом, когда писал свои сложные “кватернионные” уравнения. Позднее Оливер Хэвисайд разбил модель на четыре простых кватерниона и разрушил скрытый внутренний “потенциал” тетраэдра. Также, скрытый тетраэдр наблюдается у Уолтера Расселла, а позже у Бакминстера Фуллера. Совершая свои открытия, Джонсон не знал о предыдущих прорывах.

Следующая загадка возникает тогда, когда мы изучаем субатомные “частицы”, известные как кварки. Когда атомная структура вдруг разрушается, в пузырьковой камере появляются короткие траектории, которые будут отлетать от нормального спиралевидного пути “частицы”; они и были названы “кварками”. После высвобождения, “кварки” очень быстро исчезают. Геометрия их движений была тщательно проанализирована, поскольку единственное, что вы можете по-настоящему определить при анализе посредством пузырьковой камеры, это разные геометрические формы движения. Было открыто много разных форм “кварков”, причем каждая форма обладала разными геометрическими свойствами, ошибочно называемыми “цветом”, “шармом” и “странностью”. Мюррей Гелл-Манн первым создал единую модель, демонстрирующую как именно взаимосвязаны эти разные геометрические свойства. Он назвал ее “Восьмеричным Путем”. Замечательно, что единая геометрическая структура, которую мы видим, — тетраэдр: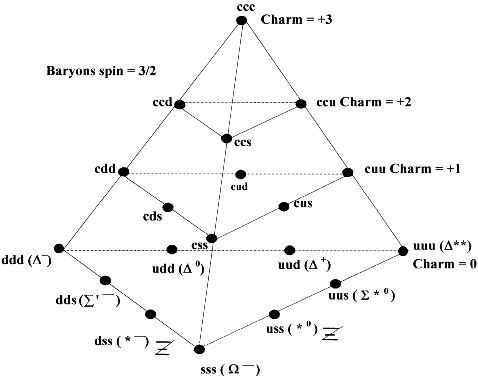

Рис. 4.9 Тетраэдр, видимый в организации “кварков” “Восьмеричного Пути” Гелл-Манна

Итак, что же мы видим? Очевидно, что каждая точка — это отдельный “кварк”. Джонсон утверждает, что “кварки” высвобождаются тогда, когда эфирный энергетический поток тетраэдра внутри атома вдруг разрушается. В течение короткого промежутка времени, высвобожденные энергетические фрагменты будут продолжать течь с теми же свойствами вращения/геометрии, которыми они обладали, будучи связанны в атоме; но они очень быстро возвращаются обратно в эфир. Разные “кварки” не следует рассматривать как возникшие в результате разрушения одного атома, поскольку угол, под которым разрушается атом, определяет, какая часть его внутреннего геометрического Единства будет высвобождена. Поэтому кварки следует тщательно изучать по отдельности. А вот что еще интереснее: в модели Гелл-Манна находятся и другие “свернутые” геометрические частоты, такие как куб-октаэдр; просто тетраэдр — это одна из трех разных открытых им иерархий.

И вновь, традиционный научный мир рассматривает Восьмеричный Путь Гелл-Манна как просто удобную геометрическую организацию, и ничего больше. В следующем отрывке д-р Мило Вольф указывает на тот факт, что геометрия могла бы быть решением для понимания структуры “ядерных пространственных резонансов” в квантовой сфере (страница 198 его книги):

“Другая интересная проблема с полезным результатом — увидеть, можно ли обнаружить способ связать ядерные пространственные резонансы с объяснением теории групп зоопарка ядерных частиц. Одно из названий этой теории — Восьмеричный Путь, открытый Гелл-Манном и Нееманом в 1960 году. Теория умно использует геометрическое группирование для определения их параметров: спина, четности, числа изотопов, числа странностей. Теория групп еще не раскрыла физическую структуру, такую как пространственные резонансы. Если связь существует, тогда логично ожидать, что решения уравнения волны пространственного резонанса обладали бы ортогональными свойствами, соответствующими Восьмеричному Пути. Волнующая перспектива”.

Интересно: когда мы заканчивали эту часть книги, с нами связался д-р Р. Б. Дункан, опубликовавший в Интернете очень детальную и основательную работу, объясняющую структуру атома с точки зрения теории групп, упомянутой выше Вольфом. Прежде, чем опубликовать решение, Дункан работал над этой проблемой тридцать лет!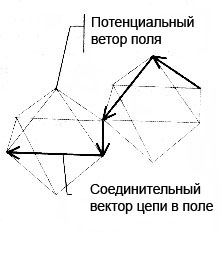

Рис. 4.10 180° углы вращения “электронов”, создаваемые импульсами, движущимися над октаэдральными энергетическими формами

Следующее положение, которое нужно рассмотреть, — спин (вращение). Много лет физики знали, что, двигаясь, энергетические частицы “вращаются”. Например, представляется, что, двигаясь в атоме, “электроны” непрерывно совершают резкие повороты на 180° или “полуспины”. Часто наблюдают, что при движении “кварки” совершают “одну треть” или “две трети” спина, что позволило Гелл-Манну организовать их движения в тетраэдр или другие геометрии. Никто из представителей официальной науки не дал адекватного объяснения, почему это происходит.

Модель Джонсона показывает, что 180° “спин” электронных облаков создается движением октаэдра, что видно на рис. 4.10. Важно осознать, что 180° движение на самом деле возникает из двух 90° поворотов каждого октаэдра. Чтобы оставаться в том же положении в матрице окружающей его геометрии, октаэдр должен “опрокинуться назад”, то есть на 180°. Тетраэдр же, чтобы остаться в том же положении, должен совершить либо 120° (одна треть спина), либо 240° (две трети спина). Более просто это будет объясняться в разделе 4.9 ниже. (Другие теоретики эфира, такие как Вольф, Крейн, Гинзбург и Красноголовец, имеют свои объяснения феномена полуспина, основанные на жидком потоке.)

Этим же процессом объясняется и загадка спиралевидного движения торсионных волн. Где бы вы ни находились во Вселенной, даже “в вакууме”, эфир всегда будет пульсировать в этих геометрических формах, образуя матрицу. Поэтому любой движущийся в эфире импульс момента будет проходить по граням геометрических “жидких кристаллов” в эфире. Следовательно, спиралевидное движение торсионной волны создается простой геометрией, через которую она должна пройти при своем движении.

Хотя мы упорно работали над тем, чтобы упростить этот раздел, визуализировать тонкоструктурную константу намного труднее. Поэтому, если вам трудно читать, его можно пропустить и перейти к итоговой части в разделе 4.10, не потеряв главную “нить” повествования книги. Мы включили этот раздел для тех, кому хотелось бы видеть, насколько далеко заходит “матричная” модель. Тонкоструктурная константа — еще один аспект квантовой физики, о котором даже не слышали некоторые представители официальной науки, возможно, потому, что она абсолютно необъяснима тем, кто склонен верить в модели, основанные на частицах.

Представьте, что электронное облако похоже на гибкий резиновый шар, и каждый раз, когда поглощается или высвобождается “фотон” энергии (что известно как спаривание), облако растягивается и изгибается, как будто дрожит. Электронное облако всегда будет “ударяться” в фиксированном, точном пропорциональном отношении к размеру фотона. Это значит: фотоны большего размера будут оказывать бо льшие “удары” на электронное облако, фотоны меньшего размера оказывают меньшие “удары” на электронное облако. Это отношение остается постоянным, не смотря на единицы измерения. Как и постоянная Планка, тонкоструктурная константа — еще одно “отвлеченное” число. Это значит, что мы будем получать одну и ту же пропорцию, не зависимо от того, в каких единицах мы ее измеряем.

Эта константа непрерывно изучалась посредством спектроскопического анализа, и в своей книге Странная теория света и материи очень уважаемый физик Ричард П. Фейнман объяснил эту загадку. (Следует помнить, что слово “спаривание” означает соединение или разделение фотона и электрона.)

“Существует очень глубокий и красивый вопрос, связанный с наблюдаемой константой спаривания e, — амплитудой реального электрона для испускания или поглощения реального фотона. Это простое экспериментально определенное число близко к 0,08542455. Мои друзья-физики его не признают, потому что им нравится запоминать это число как инверсию его квадрата — около 137,03597, с неопределенностью двух последних десятичных знаков. Оно остается загадкой и по сей день, хотя было открыто более 50 лет назад; и все хорошие физики-теоретики вешают его на стену и волнуются о нем.

Вам сразу же захотелось бы узнать, откуда пришло число спаривания: связано ли оно с π или, возможно, с основанием натуральных логарифмов? Этого никто не знает, это одна из самых великих загадок физики: магическое число, пришедшее к нам без понимания его человеком. Вы могли бы сказать, что это число начертала “рука Бога”, и “мы не знаем, как Он водил Своим карандашом”. Мы знаем, какой вид танца следует исполнять практически, чтобы очень точно измерить это число, но мы не знаем, какой вид танца следует исполнять на компьютере, чтобы вышло это число”.

В модели Джонсона проблема тонкоструктурной константы имеет очень простое академическое решение. Как мы говорили, фотон движется по двум соединенным вместе тетраэдрам, а электростатическая сила внутри атома поддерживается октаэдром. Мы получаем тонкоструктурную константу простым сравнением объемов тетраэдра и октаэдра при их соударении. Все, что мы делаем, — это делим объем вписанного в сферу тетраэдра на объем вписанного в сферу октаэдра. Мы получаем тонкоструктурную константу как разницу между ними. Чтобы показать, как это делается, требуется некоторое дополнительное объяснение.

Фазово-волновые схемы, которые мы видели раньше в этой главе (рис. 4.3 и 4.4), показали угловые соотношения между октаэдром и тетраэдром. Поскольку тетраэдр полностью треугольный, независимо от того, как он вращается, три вершины любой из его граней будут делить окружность на три равные части по 120° каждая. Следовательно, чтобы привести тетраэдр в равновесие с геометрией окружающей его матрицы, вам нужно повернуть его всего на 120°, чтобы он оказался в том же положении, что и раньше. Это легко видеть, если вы визуализируете автомобиль с треугольными колесами и хотите, чтобы он сдвигался так, чтобы колеса выглядели как раньше. Чтобы это сделать, каждое треугольное колесо должно повернуться ровно на 120°.

В случае октаэдра, чтобы восстановить равновесие, его всегда приходится переворачивать “вверх дном” или на 180°. Если вам понравилась аналогия с автомобилем, тогда колеса должны иметь форму классического “алмаза”, который вы видите на колоде карт. Чтобы алмаз выглядел точно так же, как когда вы начинали, вам придется перевернуть его вверх дном, то есть на 180°. Нижеприведенная цитата из Джонсона объясняет тонкоструктурную константу, основываясь именно на этой информации:

“(Если вы) рассматриваете статическое электрическое поле как октаэдр, а динамическое магнитное поле как тетраэдр, тогда геометрическое отношение (между ними) равно 180:120. Если вы рассматриваете их как сферы с объемами, выраженными в радианах, просто разделите их друг на друга, и вы получите тонкоструктурную константу”.

Термин “объем в радианах” означает, что вы вычисляете объем объекта через его радиус, представляющий половину ширины объекта. (Тем, кому захочется проверить математику самим: возьмите синус 180° и разделите его на синус 120°. Затем округлите число с помощью уравнения Кулона, чтобы учесть небольшую потерю энергии, которая происходит при перемещении пульсации в эфире.) Когда выполняется простой процесс деления двух “выраженных в радианах объемов”, результатом будет тонкоструктурная константа.

Интересно: после того, как Джонсон показал, что тонкоструктурную константу можно рассматривать как отношение между октаэдром и тетраэдром, как энергию, движущуюся от одного к другому, Джерри Юлиано открыл, что ее можно рассматривать как “остаточную” энергию, возникающую тогда, когда мы сжимаем сферу в куб или расширяем куб в сферу! Такие изменения расширения и сжатия между двумя объектами известны как “мозаичное размещение”, и вычисления Юлиано выполнить не трудно, просто никто не додумался сделать это раньше. В вычислениях Юлиано объем двух объектов не меняется; и куб, и сфера имеют объем 8π х π2. Когда мы сравниваем их друг с другом, разница только в величине площади поверхности. Дополнительная площадь поверхности между кубом и сферой равна точно тонкоструктурной константе.

Читатель сразу же спросит: “Как тонкоструктурная константа может быть одновременно и отношением между октаэдром и тетраэдром и отношением между кубом и сферой?” Это работа еще одного аспекта магии “симметрии”, где мы видим, что разные геометрические формы могут обладать одинаковыми свойствами, поскольку все они гнездятся одна в другой с совершенными гармоническими отношениями. Точки зрения и Джонсона и Юлиано демонстрируют, что мы имеем дело с работой геометрически структурированной энергии в атоме.

Также важно помнить, что находки Юлиано демонстрируют классическую геометрию “квадратуры круга”. Это положение долго являлось центральным элементом в эзотерических традициях “сакральной геометрии”, поскольку считалось, что оно показывает равновесие между физическим миром, представленным квадратом или кубом, и духовным миром, представленным кругом или сферой. И сейчас можно видеть, что это еще один пример “скрытого знания”, зашифрованного в метафоре так, чтобы со временем люди восстановили истинное понимание стоящей за метафорой секретной науки. Они знали: пока мы не откроем тонкоструктурную константу, мы не поймем, что наблюдаем. Именно поэтому было сохранено это древнее знание — чтобы показать нам ключ.

Сейчас, при наличии данных, которые мы видели в физике Джонсона и их реализации в науке микрокластеров, квазикристаллов и конденсатов Бозе-Эйнштейна, у нас есть единая квантовая модель. Наше изложение физики Джонсона было таким упрощенным и обтекаемым, как только можно. Поэтому любому, кто попытается проверить модель научно, потребуется прочитать дополнительный материал, чтобы познакомиться со многими нюансами. А для тех, кто обладает открытым умом, представленных нами данных больше, чем достаточно для доказательства положения. Ключ в том, что в квантовой реальности всегда существовала сакральная геометрия; просто до настоящего времени она оставалась не объясненной, поскольку традиционная наука продолжает пребывать в оковах старомодных моделей “частиц”.

В новой модели больше не нужно ограничивать атомы определенным размером; они способны расширяться и сохранять одни и те же свойства. Как только мы полностью поймем, что происходит в квантовой сфере, мы сможем создавать сверхпрочные и сверхлегкие материалы, поскольку сейчас известны точные геометрические расположения, вынуждающие атомы связываться более эффективно. Мы помним: рассказывали, что кусочки обломков крушения в Розвеле были невероятно легкими и одновременно такими прочными, что их нельзя было разрезать, сжечь или разрушить. Именно такие материалы мы сможем создавать, как только полностью поймем новую квантовую физику.

Мы помним, что квазикристаллы очень хорошо хранят тепло, часто не проводят электричество, даже если входящие в их состав металлы в нормальном виде хорошие проводники. Аналогично, микрокластеры не позволяют магнитным полям проникать внутрь самих кластеров. Физика Джонсона утверждает: такая геометрически совершенная структура обладает совершенной связью, поэтому через нее не может пройти ни тепловая, ни электромагнитная энергия. Внутренняя геометрия настолько компактна и точна, что току буквально не остается “места” для движения между молекулами.

Теперь, когда у нас есть завершенная эфирная модель квантовой физики, мы готовы двигаться вперед и показать, что эти геометрические силы продолжают оказывать влияния и на структуры крупных размеров, а именно на образования, известные как Глобальная Решетка. Бо льшая часть материала — это обзор из предыдущих книг. Тем не менее, важно рассмотреть его еще раз. Далее мы установим очень важную связь между геометрией квантов и геометрией макро, эффективно доказывая существование и важность новых теорий. Затем мы перейдем к изображению абсолютно новой модели Космоса, основанной на всех принципах, которые мы обсудили. Глава 6 будет фокусироваться преимущественно на объяснении новой космологической модели, в то время как глава 7 представит более конкретную наблюдаемую информацию, демонстрирующую новую модель в действии.

Литература

1. Besley, N.A., Johnston, R.L., Stace, A.J. and Uppenbrink, J. Theoretical Study of the Structures and Stabilities of Iron Clusters. School of Chemistry and Molecular Sciences, University of Sussex, Falmer, Brighton, BN1 9QJ, United Kingdom.

2. Carter, Barry. ORMUSand Consciousness. YGGDRASIL: The Journal of Paraphysics. 1999.

3. Carter, James. Theory of Absolute Motion.

4. Feynman, Richard P. The Strange Theory of Light and Matter.

5. Fuller, Buckminster. Planet Planning. 1969.

6. Gell-Mann, Murray. The Eight-fold Way. 1960.

7. Hartmann, Caroline. Max Planck’s Unanswered Challenge. 21st Century Science and Technology Magazine, Vol. 14, No. 2, Summer 2001.

8. Johnson, Rod and Wilcock, David. Conversations on Sequential Physics. 2001.

9. Mehrtens, Michael. Definition of Microclusters.

10. Sugano, Satoru and Koizumi, Hiroyasu. Microcluster Physics: Second Edition. Springer-Verlag, Berlin Heidelberg New York, 1998.

11. Wolff, Milo. Exploring the Physics of the Unknown Universe. Technotran Press, Manhattan Beach, CA, 1990.