Глава 3: Сакральная геометрия в квантовой реальности

Как рассказывалось в предыдущей книге, бо льшая часть космологической картины, которую мы описываем в этой книге, пришла из Ведических текстов, датирующихся 18.000-ми лет назад. Весьма похоже на то, что в древние времена вся обсуждаемая нами космология была хорошо известна Атлантам и жителям Империи Рама. Затем, приблизительно 12.000 лет назад, всемирный катаклизм разрушил обе эти цивилизации. С годами наследникам научного знания становилось все труднее и труднее видеть “большую картину”.

Почти все священные традиции, включая Веды, настаивали на существовании скрытого порядка, объединяющего все аспекты Вселенной. Также они утверждали, что при достаточном изучении и визуализации стоящих за скрытым порядком геометрических форм, ум Посвященного мог связываться с Единством Вселенной, обретал способность показывать фокусы сознания и демонстрировать преимущество сознания над материей. Визуализации одних людей принимали форму мандал, таких как Шри Янтра. Другие предпочитали танцевать, чтобы посредством движений и музыки настраиваться на эти геометрические формы. Третьим нравилось собирать, лепить и/или рисовать эти формы циркулем и линейкой, отсюда важность главного символа Массонского братства, на котором буква “G” символизировала “Геометрию” и “Великого Архитектора Вселенной”. Над буквой G располагался циркуль, а под ней — плотницкий угольник. Группы, существовавшие до Массонов, такие как Рыцари-Тамплиеры, выбирали зашифровывать геометрические отношения в своих священных структурах, таких как мозаичные окна в соборах.

Краеугольным камнем знания секретных школ мистерий, относящегося к скрытому порядку во Вселенной, всегда была сакральная геометрия. Мы достаточно писали на эту тему в двух предыдущих книгах, и для лучшего понимания просим читателя обратиться к этим двум книгам. Сакральная геометрия — это еще одна форма вибрации или “кристализованная” музыка. Рассмотрим следующий пример:

Сначала мы дергаем гитарную струну. Это создает “стоячие волны”, то есть волны, не движущиеся по струне назад и вперед, а остающиеся на одном месте. Мы увидим места, где присутствует сильное вертикальное движение, представляющее собой верх и низ волны, и другие места, где вертикального движения нет. Такие места называются узлами. Узлы, формирующиеся в любом виде стоячей волны, всегда будут расположены на одинаковом расстоянии друг от друга, а скорость вибрации будет определять количество появляющихся узлов. Это значит: чем выше вибрация, тем больше узлов.

В двух измерениях мы можем использовать осциллограф или подвергнуть вибрации плоскую круглую “пластину Хладни” и наблюдать появление узлов, формирующих простые геометрические формы, такие как квадрат, треугольник и шестиугольник. Такая работа повторялась много раз д-ром Гансом Дженни, Джеральдом Хокинсом и другими.

• Если окружность имеет три узла, расположенных на одинаковом расстоянии друг от друга, то при их соединении получится треугольник.

• Если окружность имеет четыре узла, то образуется квадрат.

• Если окружность имеет пять узлов, образуется пятиугольник.

• Шесть узлов образуют шестиугольник, и так далее.

Хотя в терминах волновой механики это очень простая концепция, Джеральд Хокинс первым математически доказал, что вписанные в окружности геометрии являются музыкальными отношениями. Мы, конечно, удивимся, узнав, что к этому открытию его привел анализ различных геометрических образований “кругов на полях”, которые появлялись буквально за одну ночь на полях английской сельской местности. Они описывались в обеих предыдущих книгах.

Самые глубинные и самые уважаемые формы священной геометрии трехмерны и известны как Платоновы Твердые Тела. Существуют только пять форм, удовлетворяющих всем необходимым правилам. Это восьмигранный октаэдр, четырехгранный тетраэдр, шестигранный куб, двенадцатигранный додекаэдр и двадцатигранный икосаэдр. На нижеприведенном рисунке тетраэдр изображен в виде “звездного тетраэдра” или сплетенного тетраэдра, что означает два тетраэдра, соединенных вместе в совершенной симметрии.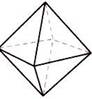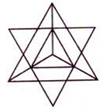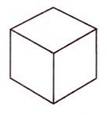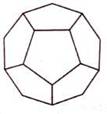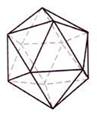

Октаэдр, Звездный тетраэдр, Куб, Додекаэдр, Икосаэдр

Рис. 3.1 — Пять Платоновых Твердых Тел

Вот некоторые основные правила этих геометрических форм:

• Каждая грань геометрического тела будет иметь одинаковую форму:

• октаэдр, тетраэдр и икосаэдр — равнобедренные треугольники,

• куб — квадраты,

• додекаэдр — пятиугольники.

• Каждое ребро каждой формы будет одинаковой длины.

• Все внутренние углы каждой формы равны между собой.

И самое важное:

• Каждая форма будет совершенно вписываться в сферу, и все вершины будут касаться сферы, не перекрывая друг друга.

Подобно двумерным случаям, включающим треугольник, квадрат, пятиугольник и шестиугольник внутри окружности, Платоновы Твердые Тела — это представления волновых форм в трех измерениях. Это положение нельзя недооценивать. Каждая вершина Платоновых Твердых Тел касается сферы в месте, где вибрации сводятся на нет, образуя узел. Следовательно, то, что мы видим, — это трехмерное геометрическое изображение вибрации/пульсации.

И студенты Бакминстера Фуллера и его протеже д-р Ганс Дженни придумали умные эксперименты, показавшие, что внутри вибрирующей/пульсирующей сферы будут формироваться Платоновы Твердые Тела. В эксперименте, проведенном студентами Фуллера, сферический воздушный шар помещался в чернила и пульсировал на “чистых” звуковых частотах, известных как диатонические звуковые отношения. На поверхности сферы образовывалось небольшое количество равноудаленных узлов и тонкие линии, соединяющие узлы друг с другом. Если будет четыре равно распределенных узла, вы увидите тетраэдр. Шесть равно распределенных узлов дадут октаэдр. Восемь равно распределенных узлов дадут куб. Двадцать равно распределенных узлов дадут додекаэдр, а двенадцать — икосаэдр. Прямые линии, которые мы видим на этих геометрических объектах, представляют напряжения, создающиеся “кратчайшим расстоянием между двумя точками” для каждого из узлов, поскольку они распределяются по всей поверхности сферы.

Рис. 3.2 — Д-р Ганс Дженни: образование Платоновых Твердых Тел в сферической вибрирующей жидкости

Д-р Ганс Дженни провел аналогичный эксперимент (небольшая часть которого приведена на рис 3.2) с каплей воды, содержащей слегка окрашенные частицы, что известно как “коллоидная взвесь”. Когда почти сферическая капля взвеси вибрировала на разных “диатонических” музыкальных частотах, внутри нее появлялись Платоновы Тела, окруженные эллиптическими кривыми линиями, соединяющими узлы. На вышеприведенном рисунке в центральной области четко видны два тетраэдра. Если бы капля была совершенной, а не сплющенной сферой, образования были бы видны еще яснее.

Тайна и значение Платоновых Твердых Тел не совсем утеряны в современной науке, поскольку эти формы удовлетворяют всем необходимым критериям для создания “симметрии” в физике многими разными способами. По этой причине они часто появляются в теориях, имеющих дело с многомерностью, когда множество “планов” должны симметрично пересекаться так, чтобы их можно было по-разному поворачивать, и чтобы они всегда оставались в одних и тех же положениях относительно друг друга. Такие теории многомерности включают “теорию групп”, так же известную как “калибровочная теория”, которая последовательно использует разные Платоновы модели для “свернутого” гипермерного пространства.

Считается, что “модулярные функции” — самый продвинутый математический инструментарий, пригодный для изучения и понимания “более высоких измерений”, на них целиком и полностью построена теория Суперструн. Уже известно, что Платоновы Твердые Тела — это ключ к открытию мира “более высоких измерений”. Помните: мы упомянули вышеуказанные положения очень кратко, поскольку они детально рассматривались в предыдущих книгах, и ключ — это симметрия. Если мы помним о симметрических качествах Платоновых Тел, тогда слова д-ра Вольфа из главы 5, озаглавленной О важности жизни в трехизмерениях, обретают весомый смысл:

Стр. 71 — “В качестве вашего наставника в исследовании, могу сказать: “Когда бы вы ни столкнулись с ситуацией симметрии в физике, остановитесь и подумайте! Потому что, воспользовавшись свойством симметрии, вы всегда будете находить более легкий способ решения проблемы. Это одна из наград в игре с симметрией. Идеи ясны…

В математике и геометрии требуется точность; поэтому симметрия определяет, что функция или геометрическая фигура остается неизменной, не смотря на: 1) поворот координат; 2) движение по оси и 3) замену переменных.

В физической науке, в которой мы заинтересованы, существование симметрии обычно означает, что закон Природы не меняется, не смотря на: 1)поворот координат в пространстве; 2) движение по оси в пространстве; 3) замену прошлого на будущее так, что t становится — t; 4) взаимную замену двух координат, такую как замену x на y, z на — z и так далее; 5) замену любой данной переменной”.

Из всех существующих форм, Платоновы Твердые Тела обладают самой совершенной симметрией, хотя здесь д-р Вольф не называет их по именам. В следующем отрывке из работы д-ра Аспдена, автор называет формирующиеся в эфире Платоновы Твердые Тела “жидкими кристаллами” и объясняет, почему они обладают действием твердых тел, даже появляясь в жидкообразной среде:

“Физики 19-го века ломали голову над эфиром потому, что он демонстрирует как свойства жидкости, так и свойства твердого тела. Таким его воспринимали с того времени, когда о “жидких кристаллах” было известно очень мало, если вообще было известно. Дисплеи многих карманных калькуляторов используют электрические сигналы и основаны на свойствах вещества, которое, подобно эфиру, демонстрирует свойства, как жидкости, так и твердого тела как функцию нарушений электрического поля.

Это убедительно объясняет, почему Тесла утверждал, что для материи эфир ведет себя как жидкость, а для света и тепла — как твердое тело. Платоновы Твердые Тела действительно ведут себя так, как будто являются структурными каркасами в эфире, организующими энергетические потоки в особые паттерны.

Отсюда, Платоновы Твердые Тела — это простые геометрические формы “кристаллизованной музыки”, естественно формирующиеся в пульсирующем эфире. Следует помнить еще одно важное положение: поскольку иерархия Платоновых Твердых Тел “растет” друг в друге, движение всегда будет происходить по спиралям, в основном в классическом отношении “фи”. Видно, что торсионные волны тоже следуют паттерну “фи”. Более подробно мы будем исследовать это в главе 9, когда будем обсуждать недооцененный феномен “силы пирамид” и “эффект полостных структур”, который первым обнаружил д-р Виктор Гребенников.

Поскольку мы только что закончили первую часть книги, далее следует обсудить новый раздел “физики микрокластеров”. Физика микрокластеров меняет точку зрения на квантовый мир, представляя абсолютно новую фазу материи, не подчиняющуюся традиционно принятым “правилам”. Микроскластеры — это крошечные “частицы”, предоставляющие явное и недвусмысленное свидетельство того, что атомы — это вихри в эфире, которые посредством вибрации/пульсации собираются в Платоновы Твердые Тела. Более того, новые открытия заводят в тупик тех, кто все еще верит в существование единичных электронов, вращающихся вокруг ядра, а не в электронные облака стоячих волн эфирной энергии, собирающиеся в геометрические паттерны. История “микрокластеров” впервые ворвалась в официальный мир науки в декабрьском 1989 года выпуске журнала Scientific American, в статье Майкла А. Дункана и Денниса Э. Роуврея:

“Дробите и дробите твердые тела, и характеристики их твердости будут исчезать одна за другой, подобно чертам Чеширского Кота, и заменяться характеристиками, не присущими ни жидкостям, ни газам. Они принадлежат новой фазе материи, микрокластеру… Они поднимают вопросы, лежащие в сердце физики твердого тела, химии и относящейся к ним области материальной науки. Насколько маленькой должна становиться совокупность частиц прежде, чем характеристика вещества, которое они когда-то образовали, исчезнет? Как могут переформировываться атомы, когда освобождаются от влияния окружающей материи? Если вещество — металл, насколько маленьким должно быть скопление атомов, чтобы избежать характерного распределения свободных электронов, лежащего в основе проводимости?”

Меньше, чем через два года наука “физика микрокластеров” обзавелась своим учебником “Физика микрокластеров”, написанным Сатори Сугано и Хирояши Коидзуми. Все цитаты из этого учебника, которыми мы будет пользоваться, приводятся из второго пересмотренного издания, вышедшего в 1998 году. В учебнике говорится: при наличии новых открытий в области микрокластеров, сейчас мы можем организовать группирования атомов в четыре основные категории размера, причем каждая категория обладает своими свойствами:

• Молекулы: 1 — 10 атомов.

• Микрокластеры: 10 — 1000 атомов.

• Тонкодисперсные включения: 1000 — 100.000 атомов.

• Уплотнение: 100.000 + атомов.

Изучая вышеприведенный список, мы ожидаем, что микрокластеры будут обладать характеристиками, общими с молекулами и тонкодисперсными включениями. На самом деле они обладают свойствами, присущими только им самим. Сугано объясняет:

“Микрокластеры, состоящие из 10–103 атомов, не демонстрируют ни свойства соответствующих уплотнений, ни свойства соответствующей молекулы, состоящей из нескольких атомов. Можно считать, что микрокластеры образуют новую фазу материи, находящуюся между макроскопическими твердыми телами и микроскопическими частицами, такими как атомы и молекулы, и демонстрирующую как макроскопические, так и микроскопические характеристики. Однако исследование новой фазы материи в развитии квантовой теории материи не проводилось вплоть до последних лет”.

По мере продолжения чтения мы узнаем, что микрокластеры не образуются случайно любой группой из 10 — 1000 атомов; только определенные “магические числа” атомов будут собираться вместе и формировать микроскластеры. Следующая цитата описывает, как это впервые было открыто. И читая, следует помнить, что упоминаемый “спектр массы” означает спектроскопический анализ, который мы обсуждали в предыдущей главе. Когда обсуждаются “кластерные лучи”, это значит, что атомы (такие как Na) пропускаются через крошечное сопло, чтобы сформироваться в луч, который затем анализируется. И самое важное: когда атомы выходят из сопла, некоторые из них спонтанно собираются в микрокластеры, демонстрирующие аномальные свойства:

“Впервые микроскопические характеристики микрокластеров были открыты посредством наблюдения аномалий спектра массы (спектрального анализа) кластерного луча натрия особых размеров. Такие размеры (количество атомов) называются магическими числами. Затем было экспериментально подтверждено, что магические числа связаны со строением оболочки коллективизированных электронов. В последние 5–7 лет наука исследования микрокластеров быстро развивалась, стимулированная эпохальными открытиями в области микрокластеров металлов и вдохновленная экспериментальными техниками, создающими относительно плотные, не взаимодействующие микрокластеры разных размеров в форме микрокластерных лучей. Также, прогресс произошел за счет усовершенствования компьютеров и вычислительных техник.

Область микрокластеров привлекает внимание многих физиков и химиков (и даже биологов), занимающихся чистыми (научными) и прикладными исследованиями, поскольку она интересна не только с чисто научной точки зрения, но и с точки зрения применения в электронике, катализе, ионной технологии, химии углеводородов, фотографии и так далее. На данной стадии развития остро ощущается необходимость вводного учебника для начинающих, поясняющего фундаментальные физические концепции, важные для изучения микрокластеров. Учебник Физикамикрокластеров удовлетворяет этим требованиям. Он базируется на ряде лекций, прочитанных аспирантам (в основном физикам) Токийского Университета, Университета Киото, Токийского Университета Метрополитен, Токийского Технологического Института и Университета Киучи в период 1987–1990 годов”.

Следующая цитата заимствована из первой части учебника Сугано и Коидзуми, где приводятся конкретные детали, касающиеся аномальных свойств микрокластеров. Хотя в терминах количества атомов микрокластеры лишь чуть-чуть меньше, чем тонкодисперсные включения, они намного более устойчивы. Здесь бо льшая устойчивость означает, что микрокластеры горят при намного более высокой температуре, чем молекулы тонкодисперсных включений тех же элементов. Согласно Дэвиду Хадсону (которого мы будем обсуждать позже), русские ученые первыми обнаружили следующее: чтобы раскрыть цветовой спектр для последующего анализа, микрокластеры должны гореть больше, чем 200 секунд, в то время как все другие известные молекулярные соединения должны гореть максимум около 70 секунд:

“Когда мы переходим к кусочку, называемому микрокластером с радиусом порядка 19 ангстрем, полученному посредством деления тонкодисперсных включений, мы видим, что следует использовать физику, отличную от физики тонкодисперсных включений. Существенное различие основано на теоретическом постулате, частично подкрепленном экспериментами, что микрокластеры данной формы и размера в принципе могут быть получены, а их свойства могут быть измерены, хотя такой вид измерения невозможен для тонкодисперсных включений. Этот постулат может подтверждаться рассмотрением факта, что кластеры данной правильной формы очень устойчивы по сравнению с кластерами других форм, количество которых довольно невелико. В противовес этому факту, тонкодисперсные включения разных форм и фиксированного размера, формирующие большие совокупности, чтобы позволить статистическую обработку, почти вырождаются энергетически. Поэтому извлечение тонкодисперсных включений данной формы не возможно.

Получено явственное свидетельство, что микрокластеры щелочи [1.8] и благородных [1.9] металлических элементов в форме кластерного луча обладают почти сферической формой и размером так называемых магических чисел. Магическое число означает особую размерность N (то есть, число атомов в кластере), при которой в спектральном анализе обнаруживается распространение аномалий. Это указывает на то, что микрокластеры таких размеров относительно устойчивы по сравнению с микрокластерами иных размеров”.

В последующих цитатах “почти сферические” формы, описанные выше, будут рассматриваться как Платоновы Твердые Тела и относящиеся к ним геометрии. Возможно, для большинства читателей следующая выдержка окажется слишком технической, поэтому ее можно пропустить; но это явное описание того, как получаются и анализируются “кластерные лучи”, и какие возникают “магические числа” атомов. Более того, следует заметить, что формирующиеся кластеры становятся электрически нейтральными — еще один аномальный и неожиданный результат:

“В качестве примера, на рис. 1.5 мы показываем спектральный анализ кластерного луча натрия. Луч создается адиабатным расширением нагретой смеси паров натрия и серебра, пропущенной через сопло. Кластеры натрия в луче фотоионизированы, спектр анализировался посредством квадрупольного спектрального анализа, и обнаруживался с помощью системы обнаружения ионов. Детальные проверки эксперимента подтвердили, что наблюдаемый спектр отражает то, что (электрически) нейтральные кластеры изначально создаются расширением струи. Аномалии распространения размера N — 8, 20, 40, 58 и 93 (рис. 1.5) — рассматриваются как магические числа нейтральных кластеров натрия”.

А теперь обратите особое внимание на следующее предложение, ибо его значимость легко можно упустить:

“Далее мы будем демонстрировать, что магические числа связаны со строением оболочки коллективизированных электронов, независимо движущихся в сферически симметричном эффективном потенциале…”

Это говорит о том, что в микрокластерах гипотетические “электроны” больше не привязаны к своим индивидуальным атомам, а движутся независимо в самом кластере! Помните, что в новой модели электронов не существует, есть только облака эфирной энергии, движущиеся к ядру посредством эффекта Бифилда-Брауна. В этом случае, микрокластер действует как один единичный атом, где центр кластера становится сродни позитивно заряженному атомному ядру, в которое втекает отрицательно заряженная энергия. Интересно: благодаря жидкообразному поведению эфира, следующий параграф позволяет предполагать, что микрокластеры могут обладать свойствами, как жидкости, так и твердого тела:

“Представляется, что (симметрия) микрокластеров металлов раскрывает следующее: аналогично атомам и молекулам, микрокластеры принадлежат к микроскопическому миру, в то время как тонкодисперсные включения принадлежат к макроскопическому миру. Это справедливо в некоторых аспектах, но не для всех. В главе 2 мы будем обсуждать, что, сталкиваясь с макроскопическим миром, при конечных внутренних температурах микрокластеры могут раскрывать жидкую фазу…”

Следующая выдержка заимствована из исследования Бисли и других, озаглавленного Теоретическое изучение структур и устойчивости кластеров железа. Очевидно, их работа не основывается на учебнике Сугано и Коидзуми. Исследование Бисли указывает на аномальные электрические и магнитные свойства, которыми обладают микрокластеры, но не обладают молекулы или конденсированная материя:

“Кластеры интересны и сами по себе, поскольку маленькие кластеры обладают вероятностью существования эффектов конечного размера, ведущих к электрическим, магнитным и другим свойствам, очень отличающимся от свойств молекул или конденсированной материи. Также было предпринято значительное исследовательское усилие, направленное на понимание геометрий, устойчивостей и химических активностей газовой фазы кластеров чистых металлов с теоретической точки зрения”.

И сейчас мы переходим к разделу 1.3.1 исследования Бисли, озаглавленному Фундаментальныемногогранники. Вот где мы обнаружим связь между микрокластерами и геометрией физики Рода Джонсона:

“Недавно обсуждалось, что устойчивые формы микрокластерам придают пять Платоновых многогранников: тетраэдр, куб, октаэдр, пятиугольный додекаэдр и икосаэдр (то есть Платоновы Твердые Тела) и два многогранника Кеплера с ромбическими гранями: ромбический додекаэдр и ромбический триаконтаэдр (тридцатигранник).

Важно отметить, что тетраэдр не заполнен пространством, как показано на рис. 1.9, а икосаэдр, диагональный додекаэдр и пятиугольный додекаэдр с пятикратной симметрией вращения не являются кристаллическими структурами: они не вырастают в периодическую структуру уплотнений. Если многогранник имеет некристаллическую структуру, тогда в период перерастания в уплотнение микрокластер вынужден подвергаться фазовому переходу в кристаллическую структуру”.

Тем, кто много лет изучал сакральную геометрию, забавно рассмотреть, что на уровне, слишком крошечном для невооруженного глаза, атомы группируются в совершенные Платоновы Твердые Тела. Также, интересно заметить, что некоторые микрокластеры обладают и свойствами жидкости, что позволяет им перетекать из одного вида геометрической структуры в другой. В своем учебнике Сугано и Коидзуми высказывают предположение, что некоторые многогранники (такие как икосаэдр и додекаэдр) не кристаллические и, следовательно, должны подвергаться фазовому изменению прежде, чем смогут стать бо льшим кристаллическим объектом. Однако позже в этой главе мы представим бесспорное свидетельство, что вся модель кристаллографии порочна, и что при определенных обстоятельствах похожие на микрокластеры образования могут формироваться на больших уровнях размера — группирования двух или более элементов.

Важно: если читатель пролистает оставшуюся часть учебника Сугано, он увидит множество изображений атомов, сгруппированных в Платоновы Твердые Тела. Мы узнаем, что в каждом случае “магическое число” группирующихся атомов будет формироваться в одну из вышеупомянутых геометрических структур. Например, если мы взяли тетраэдр и построили его из определенного количества мраморных плиток, имеющих одинаковую ширину, тогда, чтобы сложить тетраэдр данного размера, нам понадобится точное “магическое число” таких плиток. Это аналогично модели “плотно упакованных сфер” Бакминстера Фуллера, и в самой простой форме позволяет видеть, что если вы сложите три плитки вместе в виде треугольника, а затем над ним поставите четвертую плитку в середине, вы получите форму тетраэдра.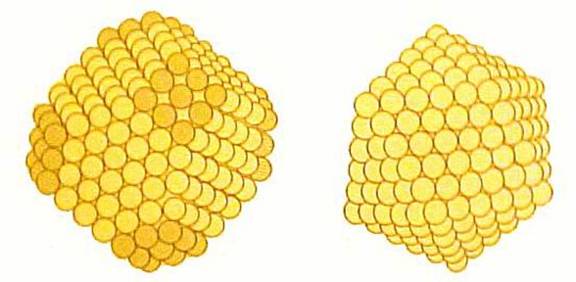

Рис. 3.3 Куб-октаэдральный кластер из 459 атомов и икосаэдральный кластер из 561 атома

И еще интереснее: на странице 18 учебника Физикимикрокластеров приводится фотография кластера золота, состоящего из “около 460” атомов. На ней можно ясно видеть плотно упакованную сферическую внутреннюю структуру атомов, образующих безошибочную геометрию. Эти изображения получены путем сканирования электронным микроскопом с очень большим увеличением. При этом в разных ракурсах четко просматривается структура куб-октаэдральной геометрии (рис. 3.3). Интересно: видно, что от рисунка к рисунку структура кластера подвергается различным геометрическим преобразованиям из куб-октаэдра в другие формы. А это свидетельствует о качестве жидкости и работе невидимых “напряжений” в эфире. Рис. 3.3 — это художественная интерпретация схемы, как “магическое число” 459 сферических атомов будет упаковываться для формирования кластера куб-октаэдральной формы, в то время как 561 атом будет собираться в форму икосаэдра.

Наша следующая цитата заимствована из раздела 3 учения Бисли и других, которое обсуждает “желеобразную” модель вещества[10] и проясняет, что индивидуальная природа атомов в микрокластере теряется в пользу группового поведения. И вновь мы столкнемся с упоминанием магических чисел и электронов, движущихся во всей структуре, вместо того, чтобы двигаться только в родительском атоме. Также мы обнаруживаем гипотезу, что “геометрические оболочки” электронов каким-то образом формируются в микрокластер.

“Для небольших кластеров простых металлов, таких как металлы оснований, масс спектроскопические исследования указывают на присутствие предпочтительных нуклеарностей или “магических чисел”, соответствующих особенно интенсивным пикам. Эти эксперименты ведут к развитию (сферической) “желеобразной” модели, где реальная геометрия кластера (то есть нуклеарные координаты) неизвестна и не важна (возможно, потому что кластеры жидкие или быстро дифференциальные), а коллективизированные электроны движутся в сферически среднем центральном потенциале. Поэтому “желеобразная” модель объясняет магические числа кластера в терминах заполнения кластерных электронных оболочек, аналогичных электронным оболочкам в атомах. Для больших нуклеарностей (N ~ 100–1500 [общее количество атомов в кластере]) существуют периодические колебания масс спектральных интенсивностей пиков, что приписывалось соединению электронных оболочек в сверхоболочки.

Долговременное наблюдение колебаний интенсивностей пиков в масс спектрах очень больших металлических кластеров (до 105 атомов) привело к выводу, что такие кластеры растут посредством формирования трехмерных геометрических оболочек атомов, и что для этих нуклеарностей сверхустойчивость кластера обеспечивается заполнением геометрией, а не электронными оболочками”.

Бесспорно, идея “сверхоболочек” электронов предполагает жидкообразное смешивание атомов в квантовой сфере. И вновь, представляется, что вся идея электронов страдает существенными недостатками, поскольку следующий параграф из работы Бисли указывает на то, что “желеобразная” модель, где электроны как “частицы” заполняют “геометрические оболочки”, не работает для того, что известно как превращение металлов. Поскольку в этой концепции не может быть индивидуальных электронов, Бисли предлагает существование “явных, зависящих от углов сил неких тел”. Короче говоря, для объяснения сил, создающих микрокластеры, требуется “жидкокристаллическая” эфирная квантовая модель:

“В случае превращения металлов нет явного свидетельства того, что имеет место “желеобразная” модель, даже для низких нуклеарностей. Мы надеемся, что модель, предлагающая явные, зависящие от углов сил некие тела (как в модели ММ [Маррела-Мотрама], которую мы заимствовали) намного лучше подходит для объяснения предпочтений кластерной структуры”.

Исходя из результатов учений о микрокластерах, не следует забывать, что Платоновы Твердые Тела очень легко формируются вибрацией сферической области жидкости. Удивительно, что исследователи микрокластеров не заметили этой связи. Преобладающее рассматривание квантовой механики как феномена частиц настолько удерживается в умах исследователей, что вынуждает разрабатывать объяснения, включающие “геометрические оболочки” электронов. Здесь ключевой вопрос таков: как и почему могли бы формироваться эти геометрии. И идея вибрирующей жидкообразной квантовой среды была бы самым простым ответом. Микрокластер — это просто больший “эфирный атом” в совершенной геометрической форме.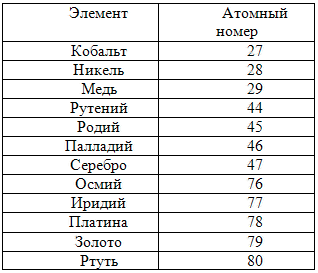

Таблица 3.1 Известные металлические микрокластеры или “ОТМЭ” в патенте Дэвида Хадсона

Мы представляем работу Дэвида Хадсона. В конце 1970-х годов на личном золотом прииске он открыл вещество, предположительно, содержащее микрокластеры. На анализ и проверку этих загадочных материалов Хадсон потратил несколько миллионов долларов, и в 1989 году запатентовал открытие микрокластеров, назвав их Орбитально-Трансформированными Одноатомными Элементами или “ОТМЭ”. В начале 1990-х годов, в опубликованных лекциях, Хадсон демонстрирует обширное знание физики микрокластеров, но его открытия более спорны, чем те, что мы находим в учебнике Сугано и других опубликованных источниках. Патент Хадсона фокусируется на микрокластерных структурах, обнаруженных в вышеприведенных элементах благородных металлов. Здесь следует отметить: Сугано и Коидзуми утверждали, что микрокластеры обнаруживались и в не металлических элементах.

Хадсон открыл, что все вышеприведенные микрокластерные металлы в изобилии существуют в морской воде. И что еще более удивительно, он обнаружил, что на Земле в микрокластерном состоянии эти элементы присутствуют в 10.000 раз больше, чем в обычном металлическом состоянии. Хадсон продемонстрировал, что эти металлические микрокластеры обнаруживаются во многих различных биологических системах, включая многие разные растения, и формируют до 5 % веса материала мозга. Более того, при комнатной температуре они работают как сверхпроводники, обладают качествами суперполя и левитируют в присутствии магнитных полей, поскольку магнитная энергия не может проникать через их внешние оболочки. Их физические качества соответствуют описаниям различных материалов в алхимических традициях Китая, Индии, Персии и Европы. Многие люди добровольно глотали микрокластеры золота или “одноатомное золото” и сообщали о тех же эффектах, что и при изменениях кундалини, описанных в Ведических текстах древней Индии.

Еще более спорны открытия Хадсона, связанные с нагреванием микрокластеров иридия. При нагревании вес материала увеличивался на 300 % и даже больше. И вот что самое удивительное: когда микрокластер иридия нагревается до температуры 850° Цельсия, материал исчезает из физической реальности и теряет весь свой вес. Однако при понижении температуры, микрокластер иридия появляется вновь и восстанавливает большую часть исходного веса. В патенте Хадсона есть таблица, разработанная посредством термо-гравиметрического анализа, которая демонстрирует действие этого эффекта.

Идея о материале, увеличивающем вес, затем спонтанно его теряющем и исчезающем из физической реальности, больше не должна казаться чем-то необычным, если мы объединим находки Козырева, изменения Гинзбурга, внесенные в традиционные уравнения относительности, и открытия Мишина и Аспдена о множественности плотностей эфира. Козырев показал, что нагревание или охлаждение объекта может влиять на его вес небольшим, но измеряемым образом. Также мы видели, что увеличение или уменьшение веса происходит внезапными “квантованными” скачками, а не плавно и постепенно. Д-р Владимир Гинзбург предположил, что, приближаясь к скорости света, масса объекта превращается в чистое поле, а данные Мишина и Аспдена позволяют полагать, что масса перемещается в более высокую плотность эфирной энергии.

Таким образом, наблюдаемые и запатентованные Хадсоном эффекты с микрокластером иридия обеспечивают первое (в этой книге) главное доказательство идеи о том, что объект может полностью перемещаться в более высокую плотность эфирной энергии. В случае с микрокластером иридия, представляется, что геометрическая структура микрокластера позволяет воспользоваться тепловой энергией намного более интенсивно. Кроме того, использование вибраций тепла создает особый резонанс при относительно более низкой температуре, вынуждая внутренние вибрации иридия превышать скорость света. (Внутренние вибрации уже могут быть относительно близки к скорости света и до введения дополнительного резонанса, благодаря скорости, с которой эфир течет через атомный “вихрь” отрицательных электронных облаков и положительного ядра.) Затем, когда, наконец, достигается пороговая точка скорости света, эфирная энергия иридия перемещается в более высокую плотность и исчезает из физической реальности. Когда температура понижается, иридий вновь возвращается в нашу плотность, поскольку давление, удерживающее его в более высокой плотности, исчезает.

Сейчас, осветив аномальную сферу микрокластеров, мы готовы приняться за более традиционно понимаемые проблемы строения кристалла. Обыкновенная столовая соль — совершенный пример того, как два разных элемента (натрий и хлор) связываются вместе и формируют геометрию Платоновых Твердых Тел; в данном случае куб. Два атома водорода и один атом кислорода соединяются в форме тетраэдра и образуют молекулу воды (которая в жидком состоянии кристаллом не является, но обладает тетраэдральной молекулой). Кристаллы флюорита образуют октаэдр. Кристаллы, формирующиеся с такими свойствами, будут сохранять одинаковую ориентацию и симметрию. Более техническое описание: кристаллы — это “твердые тела, обладающие плоскими поверхностями (гранями), пересекающимися под характерными углами, и упорядоченными на микроскопическом уровне”. Здесь ключевой вопрос был бы таков: “Почему сферические энергетические вихри соединяются под такими характерными геометрическими углами и паттернами?” И конечно, ответ будет найден в понимании Платоновых Твердых Тел как “гармонических” энергетических структур в эфире.

Классическое определение Глускера и Трублада, как образуются кристаллы, следующее: они образуются посредством:

“… регулярно повторяющегося расположения атомов. Любой кристалл может рассматриваться как состоящий из непрерывного, трехмерного поступательного повторения некоего основного структурного паттерна”.

Термин “поступательный” означает, что мы поворачиваем конкретный объект на точное число градусов, такое как 180, что сформировало бы “двойной” кристалл, поскольку в круге из 360° будет два таких поворота. Таким образом, “поступательное повторение” означает, что для формирования повторяющегося паттерна базовый структурный элемент (атом или молекулярная группа атомов), составляющий кристалл, может одинаково поворачиваться вновь и вновь. Технический термин для регулярного расположения — периодичность. Это значит, что кристалл состоит из “определенной базовой структурной единицы, повторяющейся бесконечно во всех направлениях и заполняющей все пространство” внутри себя. Одинаковая структура (атом или группа атомов) сохраняется, повторяясь одинаковым, периодичным способом; отсюда термин “периодичность”.

В классической теории “периодического” кристалла каждый атом сохраняет исходный размер и форму, и не влияет ни на какие атомы, за исключением тех, с которыми непосредственно связан.

Важно осознать, что в кристаллографии модель периодичности работает очень хорошо. Посредством этого метода можно анализировать любой обнаруженный вид кристалла, и основываясь на простых геометрических принципах, можно предсказать углы между всеми гранями. В 1912 году Макс фон Лое открыл способ использовать рентгеновские лучи для просвечивания внутренней структуры кристаллов, создавая то, что известно как “дифракционная картинка”. Картинка появляется в виде расположения отдельных точек света на темном фоне. Это привело к появлению целой науки — рентгеновской кристаллографии, формализованной Уильямом Г. и Уильямом Л. Брэггами. Для определения истинной структуры кристалла, точки света геометрически анализируются по отношению друг к другу. На протяжении семидесяти лет после создания этой технологии, каждая дифракционная картинка, когда-либо наблюдавшаяся традиционными учеными, совершенно вписывалась в модель периодичности. И это неминуемо привело к очень простому выводу: все кристаллы являются расположением единичных атомов как структурных единиц.

Одно из математических правил, относящихся к модели периодичности, гласит: кристалл может иметь только 2-х, 3-х, 4-х и 6-ти кратные вращения (повороты). В этой модели, если у вас есть кристалл, состоящий из единичных атомов или молекул в повторяющейся периодической структуре, он не может иметь пятикратное вращение или любое вращение выше 6-ти. “Считается”, что атомы обладают индивидуальными точечными особенностями и не сливаются с другими атомами в большее целое. Тем не менее, в терминах чистой геометрии, додекаэдр обладает пятикратной симметрией, а икосаэдр имеет 5-ти и 10-ти кратную симметрию. Эти Платоновы Твердые Тела удовлетворяют всем требованиям симметрии, описанным д-ром Вольфом. Просто для создания таких форм вы не можете сложить вместе единичные атомы. Итак, вновь, додекаэдр и икосаэдр обладают симметрией, но не обладают периодичностью как кристаллы. Следовательно, в науке не существует основания полагать, что любая из этих форм появилась бы в виде молекулярной кристаллической структуры, это просто “не возможно”. Или они так думали…

А теперь перейдем к малоизвестному крушению в Розвеле (штат Нью-Мексико). Согласно бывшему работнику Groom Lake/Area 51 Эдгару Фуше, на восстановленном твердом диске были обнаружены молекулярные структуры, не укладывающиеся в традиционную модель периодичности кристалла. Эти структуры стали известны как “квазикристаллы”, сокращенное от словосочетания “почти периодические кристаллы”. В этих уникальных сплавах появлялись и икосаэдр и додекаэдр. Было открыто: подобно микрокластерам, только на большем уровне размера, квазикристаллы обладают многими странными свойствами. Это и сверхпрочность, и сверхсопротивление нагреванию, и не проведение электричества, даже если входящие в их состав металлы обычно работают как проводники! В отличии от микрокластеров, казалось бы, способных только индивидуально формироваться из “кластерных лучей”, квазикристаллы могут группироваться в удобные сплавы. У себя на сайте Фуше констатирует следующее:

“Благодаря своей должности в военно-воздушных силах США, я имел доступ к самым высшим секретам государства.

В разговорах в (секретном) зале Groom я слышал слова: силы Лоренца, пульсирующие детонации, циклотронное излучение, полевые генераторы трансдукции (переносы генетического материала) квантового потока, квазикристаллические энергетические линзы и квантовые приемники электронного парамагнитного резонанса. Мне говорили, что квазикристаллы — ключ к целой новой области технологии движущих сил и коммуникации.

И по сей день, мне не разрешают объяснить уникальные электрические, оптические и физические свойства квазикристаллов, и почему большая часть исследований засекречена.

Четырнадцать лет изучения квазикристаллов позволили выявить существование множества устойчивых и сверхустойчивых квазикристаллов с 5-ти, 8-ми, 10-ти и 12-ти кратной симметрией, странными структурами (такими как додекаэдр и икосаэдр) и интересными свойствами. Для изучения и описания этих необычных материалов требуется создание новых инструментов.

Я обнаружил следующее: секретное исследование показало, что квазикристаллы — это многообещающие кандидаты в материалы для хранения высокой энергии, металлических матричных компонентов, термальных барьеров, экзотических покрытий, инфракрасных сенсоров, использования высоко мощных лазеров и электромагнетизма. Некоторые высоко прочные сплавы и хирургические инструменты уже есть на рынке. (Примечание: В 1993 году лично Уилкоку сказали, что тефлон и кевлар — продукты реверсивной технологии.)

Одна из историй, которую я слышал не единожды, такова: одной из кристаллических пар, используемых для движения потерпевшего крушение в Розвеле аппарата, был кристалл водорода. До последнего времени, создание кристалла водорода превышало достижения нашей науки. Сейчас все изменилось. В одной сверхсекретной Черной Программе метод производства кристаллов водорода был раскрыт, и производство началось в 1994 году.

Решетка квазикристаллов водорода и другого не названного материала служила основой для плазменного двигателя аппарата Розвела и являлась неотъемлемой частью био-химической технологии средства передвижения. Огромная часть продвинутой кристаллографии, о которой даже не мечтали ученые, была открыта учеными и инженерами, которые оценивали, анализировали и пытались воссоздать технологии, использованные в аппарате Розвела и семи космических кораблях, потерпевших крушение после Розвела”.

Весьма вероятно, что после 34-летнего секретного исследования жесткого диска Розвела, у восстановивших эти технологии все еще имеются сотни, если не тысячи, вопросов без ответов о том, что они нашли. В целях “безопасности” было решено потихоньку ввести квазикристаллы в не посвященный научный мир. Сейчас Интернет буквально кишит тысячами разных ссылок на квазикристаллы, абсолютно лишенных какого-либо упоминания о микрокластерах. (Ни одна из статей, которые нам удалось обнаружить в сети, не упоминает микрокластеры и квазикристаллы в одной и той статье.) Многие ссылки на квазикристаллы поступают от компаний, являющихся государственными подрядчиками, и легко видеть, что эта область интенсивно изучается. Однако о ней почти не упоминается в средствах массовой информации, хотя квазикристаллы представляют собой уникальную проблему для превалирующих теорий квантовой физики. Исследование продолжается, но с тщательно подавляемым волнением.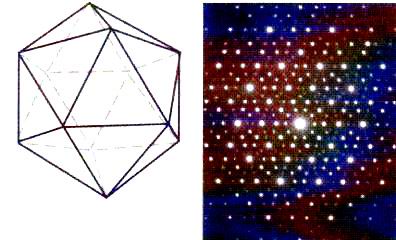

Рис. 3.4 Икосаэдр (слева) и рентгеновская диффракционная картинка квазикристалла

8 апреля 1982 года Дэну Шехтману была оказана честь/обязанность “открыть“ (или дано разрешение открыть) квазикристаллы на примере сплава алюминия с марганцем (Al6 Mn), который начинался в расплавленном жидком состоянии, а затем очень быстро остывал. На рентгеновской дифракционной картинке были обнаружены кристаллы в форме икосаэдра, похожие на вышеприведенное изображение. Данные Шехтмана не публиковались вплоть до ноября 1984 года! На рисунке 3.4 (справа) можно четко видеть ряд пятиугольников, указывающих на пятикратную симметрию икосаэдра.

Как мы говорили, с приходом квазикристаллов, появляются додекаэдр и икосаэдр, наряду с другими необычными геометрическими формами. И это завершает появление в квантовой сфере всех пяти Платоновых Твердых Тел. И додекаэдр и икосаэдр обладают элементами пятикратной симметрии в пятигранных структурах. Рис. 3.5 от Ан Панг Цая (Япония) показывает квазикристалл сплава алюминий-медь-железо в форме додекаэдра и сплав алюминий-никель-кобальт в форме декагональной (десятисторонней) призмы:

Рис. 3.5 Додекаэдральная (справа) и декагональная (слева) призма квазикристаллов, созданных Ан Панг Цаем

Проблема в том, что вы не можете создать такие кристаллы, используя единичные связанные вместе атомы; и все же на фотографиях мы видим, что они весьма реальны. Тогда ключевая проблема ученых, как объяснить и охарактеризовать процесс, посредством которого формируются эти кристаллы. Согласно А. Л. Мэки, одним из способов включить пятикратную симметрию в определение кристалла является “ликвидация атомности”:

“Фрактальные структуры с пятикратными осями требуют ликвидации атомов конечного размера. Для кристаллографов всего мира это не рациональное допущение, но математики могут свободно его исследовать”.

Это позволяет предположить следующее: представляется, что аналогично микрокластерам, квазикристаллы больше не обладают индивидуальными атомами, скорее атомы слились в единство во всем кристалле. И хотя кристаллографов будут терзать сомнения, это одно из четырех самых простых решений проблемы (А. Л. Мэки), поскольку вовлекает простую трехмерную геометрию и сочетается с наблюдениями микрокластеров. И вновь, поскольку кристаллы весьма реальны, остается преодолеть единственное главное препятствие — веру в то, что атомы состоят из частиц.

Другой относящийся к теме пример — конденсат Бозе-Эйнштейна. Он был открыт в 1925 году Альбертом Эйнштейном и индийским физиком Сатьендранатом Бозе, и впервые продемонстрирован в газе в 1995 году. Короче говоря, конденсат Бозе-Эйнштейна — это большая группа атомов, ведущих себя как отдельная “частица”, где каждый составляющий ее атом одновременно занимает все пространство и все время во всей структуре. Измерено, что все атомы вибрируют на одной и той же частоте, движутся с одинаковой скоростью и расположены в одной и той же области пространства. Разные части системы действуют как единое целое, теряя все признаки индивидуальности. Именно такое свойство требуется для существования “сверхпроводника”. (Сверхпроводник — это субстанция, проводящая электричество без потери тока.)

Обычно, конденсат Бозе-Эйнштейна может формироваться при крайне низких температурах. Однако подобные процессы мы наблюдаем в микрокластерах и квазикристаллах, которые лишены индивидуальной атомной идентичности. Интересно, еще один подобный процесс — действие света лазера, известного как “когерентный” свет. В случае лазера, в пространстве и времени весь лазерный луч ведет себя как единичный “фотон”, то есть, в лазерном луче нет способа выделить в нем индивидуальные фотоны. Интересно отметить, что лазеры, сверхпроводники и квазикристаллы обнаруживались в реверсивных технологиях инопланетян с 1940-х годов.

Естественно, это возвращает весь мир новой квантовой физики к дискуссионному столу. Представляется, что со временем квазикристаллы и конденсаты Бозе-Эйнштейна будут широко использоваться и пониматься как примеры того, что, свернув на дорогу квантового мышления, основанного на “частицах”, мы сбились с пути. Более того, в конце 1960-х годов английский физик Герберт Фрёлих предположил, что живые системы часто ведут себя как конденсаты Бозе-Эйнштейна, только в крупном масштабе.

Наш следующий вопрос касается “электронных облаков”, наблюдаемых в атоме. И Род Джонсон и Дэн Винтер отмечали, что в атоме “электронные облака” тетраэдральной формы будут совершенно соответствовать граням Платоновых Твердых Тел. Винтер называет “электронные облака” “вихревыми конусами”. Рис. 3.6 — это, к сожалению, неразборчивая копия Периодической Таблицы Элементов, разработанной Сэром Уильямом Круксом[11] — хорошо известным и высоко уважаемым ученым начала 20-го века, позже ставшим исследователем в области парапсихологии. Внизу рисунка мы видим иллюстрацию того, как “вихревые конусы” соответствуют каждой грани Платоновых Твердых Тел.

Атомная таблица согласно Круксу, где Платоновы формы вмещают вихревые конуса, определенные симметричными группами (валентностью)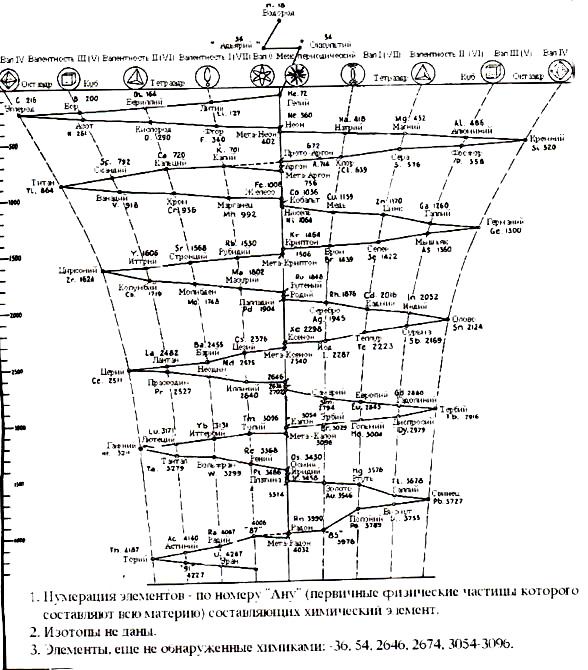

Рис. 3.6 Геометрическая Таблица Элементов Сэра Уильяма Крукса, перепечатанная Дэном Винтером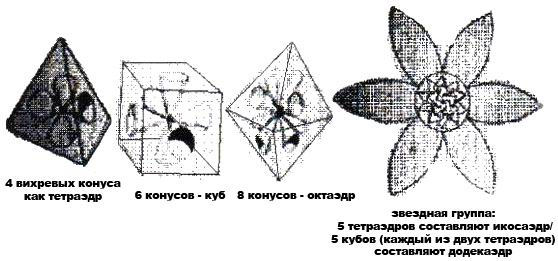

(Представляется, что более удобочитаемая копия рис. 3.6 может находиться в ранних книгах Винтера. Названия одних элементов можно увидеть, рассматривая рисунок в полный размер, названия других могут быть выведены, исходя из их расположения относительно известной Периодической Таблицы Элементов. Очевидно, таблица читается сверху вниз, и первый элемент, ниже двух кругов в центре, — гелий, затем линия движется к каждому последующему элементу. Масштаб слева — ряд угловых измерений, начинающихся с 0 на верхней линии и отсчитываемых единицами в 10° для каждой линии. Числа градусов, обозначенных на шкале, — 50, 100, 150, 200, 250, 300, 350 и 400. Представляется, что это указывает на то, что теория Сэра Крукса включает ряд угловых поворотов или переводов элементов в терминах их геометрии, когда мы движемся от одного элемента к другому. Можно видеть, что волна в основном прямая, временами на линии есть “понижения”, по-видимому, соответствующие большему угловому повороту, который пришлось сделать.)

Если вернуться к тому, что писал д-р Аспден о Платоновых Твердых Телах в эфире: он установил, что они работают как “жидкие кристаллы”, что означает: они ведут себя как твердые тела и как жидкости одновременно. Поэтому, как только мы понимаем, что размещение электронных облаков определяется невидимыми Платоновыми Твердыми Телами, становится легче увидеть, как формируются кристаллы и даже как можно получить квазикристаллы. В атоме существуют “гнезда” Платоновых Твердых Тел, одно тело для каждой основной сферы в “гнезде”. Также на разных уровнях валентности “гнезда” электронных облаков сосуществуют. Платоновы Твердые Тела формируют энергетическую структуру и каркас, по которому должна течь эфирная энергия, поскольку она “спешит” в положительный центр атома, где давление низкое. Отсюда, мы рассматриваем каждую грань Платоновых Тел как воронку, через которую должна проходить энергия, создавая то, что Винтер назвал “вихревыми конусами”.

Концепции Джонсона о Платоновой симметрии в структуре атомов и молекул, рассматриваемые в следующей главе, не должны казаться нам странными, какими они бы показались большинству людей. При наличии того, что мы уже видели, наряду с исчерпывающим исследованием, описанным в этой главе (особенно технология квазикристаллов), представляется, что эта информация уже используется человечеством в определенных кругах.

Литература

1. Aspden, Harold. Energy Science Tutorial # 5. 1997.

2. Crane, Oliver et al. Central Oscillator and Space-Tine Quanta Medium. Universal Expert Publishers, June 2000, English Edition.

3. Duncan, Michael A. and Rouvray, Dennis H. Microclusters. Scientific American Magazine, December 1989.

4. Fouche, Edgar. Secret Government Technology. Fouche Media Associates, Copyright 1998/99.

5. Hudson, David. ORMUS Elements.

6. Kooiman, John. TR — 3B Antigravity Physics Explained. 2000

7. Mishin, A. M. Levels of aetheric density.

8. Winter, Dan. Braiding DNA: Is Emotion the Weaver? 1999.

9. Wolff, Milo. Exploring the Physics of the Unknown Universe. Technotran Press, Manhattan Beach, CA, 1990.

Примечания:

1

1 http://www.philosophy.ru/library/plato/tim.html Диалог Тимей написан Платоном около 360 г до н. э. Он посвящен космологии, физике и биологии.

10

10 Желеобразная модель вещества представляет каждый кластер в виде капельки вязкого желе, внутри которой может свободно перемещаться только один электрон от каждого атома натрия.

11

11 К счастью, более разборчивую копию удалось найти в электронной версии книги Джинараджадаса по адресу: http://kosmoritm.narod.ru/him1.htm. Очень интересно: предлагается версия строения материя согласно представлениям ясновидящим.