Одной из отличительных черт бурного развития науки является широкое применение статистических методов и вычислительной техники в освоении информации. В настоящее время невозможно представить себе дисциплину, которая не пользовалась бы в процессе познания методами численного выражения закономерностей, связей, зависимости, измерения тенденции и т. д. Это, в частности, относится и к экономическим наукам.

В статистической литературе большое внимание уделяется изучению и применению отдельных статистических методов и приемов, но совсем недостаточно освещены вопросы целесообразности и последовательности использования того или иного статистического метода, их комплексного применения, сочетания различных методов. Абсолютизация того или иного метода исследования ничего, кроме вреда, не приносит. Только сочетание различных методов может дать заметный эффект. Именно с этих позиций и нужно оценивать роль и место статистического моделирования в системе познания различных процессов и явлений. В данной работе предпринята попытка систематизировать методику комплексного применения статистических методов в экономических исследованиях, рассмотрена целесообразность и последовательность использования статических методов и приемов при анализе статических и динамических процессов.

Первым этапом исследования является накопление (сбор) необходимых сведений об изучаемом объекте. Если наблюдений не очень много, то можно провести упорядочение, расположив их в порядке возрастания или убывания, т. е. построить ранжированные ряды. Если же наблюдений много, то приходится прибегать к их группировке. Статистические ряды носят самый разнообразный характер, имеют различное назначение и в разных целях могут использоваться в экономическом анализе. Одни статистические ряды являются вариационными рядами распределения. Эти ряды показывают распределение единиц изучаемой совокупности по отдельным группам, выделенным по какому-либо признаку. Другой разновидностью статистических рядов является последовательность чисел, отражающих величину того или иного показателя во времени. Это так называемые ряды динамики. Они позволяют анализировать изменение любых явлений во времени, об этом речь пойдет позже. Не умаляя значения временных рядов, следует отметить, что вариационным рядам распределения в статистическом анализе принадлежит особое место, ибо только при помощи распределения сложных совокупностей на качественно однородные группы можно изучать их структуру, соотношение между частями целого и т. п., без чего немыслим никакой экономический анализ. Ряды распределения могут строиться по качественным (атрибутивным) и по количественным признакам, по одному признаку и по нескольким, предоставляя тем самым широкие возможности исследователям при изучении сложных экономических явлений. Ряды распределения могут быть представлены либо в табличной форме, либо в геометрической, т. е. графической. Статистическая совокупность, представленная в виде ранжированного ряда распределения, графически изображается в виде огивы. Она строится так: на оси абсцисс наносятся номера элементов совокупности по ранжиру, а на оси ординат откладываются значения признака. Огива наглядно показывает интенсивность изменения изучаемого признака. Вариационные ряды распределения изображаются графически в виде полигонов и гистограмм. В виде полигонов обычно изображаются дискретные вариационные ряды распределения. При этом значения признака откладывают на оси абсцисс, а частоты (или частости) – на оси ординат. Вершины ординат соединяют прямыми линиями, в результате чего получают полигон (многоугольник). В виде полигона можно представить и интервальные вариационные ряды. Для этого за отдельные значения признака принимаются средние значения интервалов. Интервальные же вариационные ряды чаще всего изображают в виде гистограммы, в которой частоты выражают в виде прямоугольников соответствующей длины, а основания прямоугольников, опирающиеся на ось абсцисс, соответствуют интервалу значения признака (рис. 1).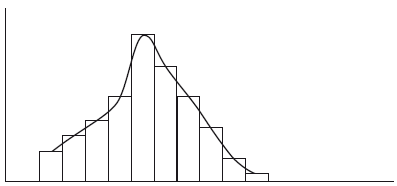

Рис. 1. Гистограмма и полигон распределения

Различают одновершинные и многовершинные распределения. Многовершинность распределения, как правило, является признаком неоднородности изучаемой совокупности. Из разнообразия форм одновершинных кривых распределений можно выделить следующие наиболее характерные типы: симметричные, умеренно асимметричные, крайне асимметричные.

В практике обычно редко встречаются идеально симметричные распределения, чаще умеренно асимметричные, в которых частоты с одной стороны от центра рассеивания уменьшаются заметно быстрее, чем с другой. Асимметричное распределение в пределе становится крайне асимметричным – в этом случае наибольшая частота расположена на одном из концов распределения.

При решении некоторых вопросов удобнее пользоваться накопленными частотами распределения. Кривая накопленных частот распределения носит название «кумулята распределения». При построении кумуляты на оси абсцисс откладываются значения признака, на оси ординат – накопленные частоты. Построение вариационного ряда распределения и его графическое изображение позволяют получить первое представление о его наиболее характерных общих чертах. В то же время статистическое изучение совокупности не может ограничиться лишь простым упорядочением наблюдаемых величин. К тому же ряды распределения и их графики бывают довольно громоздкими, так как включают в себя всю исходную информацию. Поэтому наиболее рациональным путем статистического описания распределения будет вычисление определенных числовых характеристик, отражающих реальные свойства совокупности. К таким характеристикам прежде всего относятся характеристики центральной тенденции ряда распределения, т. е. нахождение его центрального значения; рассеивания значений признака относительно центра распределения; асимметрии и островершинности распределения. Изучение статистических характеристик распределений целесообразно начать с рассмотрения наиболее простых и в то же время чаще всего используемых в статистическом анализе, т. е. с изучения средних величин; затем научиться измерять вариацию, изучить меры скошенности и островершинности. Все эти показатели тех или иных особенностей распределения составляют единую систему статистических характеристик.

Однако применение тех или иных статистических методов предполагает прежде всего однородность изучаемой совокупности: нельзя, например, анализировать совокупность, состоящую из разных категорий хозяйств, включающую предприятия разной специализации и т. д. Для успешного решения задач необходимо глубокое понимание сущности изучаемого процесса или явления. Учитывая сложность, неоднородность экономических явлений и процессов, необходимо производить анализ таким образом, чтобы наиболее существенные различия между отдельными группами явлений не затушевывались, а выделялись для более успешного их изучения. В то же время объединение в группы сходных однотипных явлений помогает выявить их черты и особенности, которые при изучении каждого явления отдельно могут оставаться незамеченными. Выделение в каждой совокупности общественно/экономических типов явлений – главное условие ее научного анализа. А это можно осуществить, только применяя метод типологических группировок.

Массовые явления хозяйственной деятельности предприятий, являющиеся объектом статистического изучения, имеют сложный характер, обладают качественной общностью, свойственной данному явлению, но в то же время имеют и различия. Так, производством какой-либо продукции занимаются сельскохозяйственные предприятия и фермерские хозяйства и т. д. Стало быть, при характеристике производства данного вида продукции в регионе следует исходить из учета качественных особенностей предприятий, производящих эту продукцию, – в противном случае выводы будут неточными, а принимаемые на основании таких выводов решения – неэффективными.

Типологическая группировка данных – основной прием изучения экономических явлений, обеспечивающий качественную сопоставимость единиц совокупности и дающий возможность получения обобщенного количественного значения признака.

Метод группировок позволяет изучить состояние и взаимосвязи экономических явлений, если группы будут охарактеризованы показателями, раскрывающими наиболее существенные стороны изучаемого явления.

При анализе и планировании необходимо опираться не на случайные факты, а на показатели, выражающие основное, типичное, коренное. Такую характеристику дают различные виды средних величин, а также мода и медиана.

Вопрос об однородности совокупности не должен решаться формально по форме ее распределения. Его, как и вопрос о типичной средней, нужно решать, исходя из причин и условий, формирующих совокупность. Однородной является такая совокупность, единицы которой формируются под воздействием общих главных причин и условий, определяющих общий уровень данного признака, характерный для всей совокупности.

Согласно теории типологических группировок, решающее значение в оценке однородности совокупности принадлежит не форме распределения, а размеру вариации и условиям ее формирования. Для качественно однородной совокупности характерна вариация в определенных пределах, после чего начинается новое качество. Вместе с тем к этим границам для оценки качественной однородности совокупности надо подходить с точки зрения существа дела, а не формально, так как одно и то же количество в разных условиях выражает новое качество. Например, при одной и той же численности рабочих предприятия одних отраслей промышленности являются крупными, а других – мелкими.

Для всестороннего и углубленного изучения явлений, для объективной характеристики типов явлений, их взаимоотношений и процессов, обусловленных развитием системы как целого, необходимо сочетать групповые средние с общими средними. Сочетание таких средних и является одним из основных элементов анализа сложных систем. Это сочетание связывает в одно целое два органически дополняющих друг друга статистических метода: метод средних величин и метод группировки. При расчете средней индивидуальные варьирующие по группе значения заменяются одним средним значением. При этом случайные отклонения значения признака по отдельным единицам в сторону увеличения или уменьшения взаимно уравновешиваются и погашают друг друга, а в величине средней проявляется типичный размер признака, свойственный данной группе. Средняя величина служит характеристикой совокупности и в то же время относится к отдельному ее элементу – носителю качественных особенностей явления. Значение средней вполне конкретно, но одновременно и абстрактно; оно получено путем абстрагирования от случайного индивидуального по каждой единице с целью выявления того общего, типичного, что свойственно всем единицам и что формирует данную совокупность. При расчете средней величины численность единиц совокупности должна быть достаточно большой. Величина средней определяется как отношение общего объема явлений к числу единиц совокупности в группе. Для несгруппированных данных это будет средняя арифметическая простая:

а для сгруппированных данных, где каждое значение признака имеет свою частоту, – средняя арифметическая взвешенная:

где X_i – значение признака; f_i – частота этих значений признака.

Поскольку средняя арифметическая рассчитывается как отношение суммы значений признака к общей численности, она никогда не выходит за пределы этих значений. Средняя арифметическая обладает рядом свойств, которые широко используются в целях упорядочения расчетов.

1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю: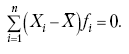

Доказательство. n

Разделив левую и правую часть на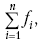

 получим: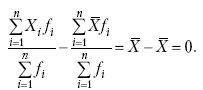

2. Если значения признака (X_i) изменить в k раз, то средняя арифметическая также изменится в x раз.

Доказательство.

Среднюю арифметическую из новых значений признака обозначим X, тогда: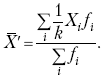

Постоянную величину 1/k можно вынести за знак суммы, и тогда получим: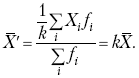

3. Если из всех значений признака X_i вычесть или прибавить одно и то же постоянное число, то средняя арифметическая уменьшится или увеличится на эту величину.

Доказательство.

Средняя из отклонений значений признака от постоянного числа будет равна: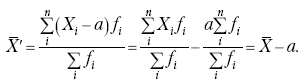

Точно так же доказывается это и в случае прибавления постоянного числа.

4. Если частоты всех значений признака уменьшить или увеличить в n раз, то средняя не изменится: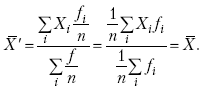

При наличии данных об общем объеме и известных значениях признака, но неизвестных частотах для определения среднего показателя используют формулу среднеарифметической взвешенной.

Например, имеются данные о ценах реализации капусты и общей выручке за различные сроки реализации (табл. 1).

Таблица 1.

Цена реализации капусты и общая выручка за различные сроки реализации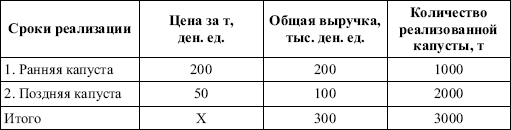

Так как средняя цена представляет отношение общей выручки к общему объему реализованной капусты, то вначале следует определить количество реализованной капусты по разным срокам реализации как отношение выручки к цене, а затем уже определить среднюю цену реализованной капусты.

В нашем примере средняя цена будет: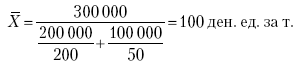

Если рассчитать в данном случае среднюю цену реализации по средней арифметической простой, то получим иной результат, который исказит истинное положение и завысит среднюю цену реализации, так как не будет учтен тот факт, что большая доля в реализации приходится на позднюю капусту с более низкой ценой.

Иногда требуется определить среднюю величину, когда значения признака даются в виде дробных чисел, т. е. обратных целым числам (например, при изучении производительности труда через обратный его показатель, трудоемкость). В таких случаях целесообразно использовать формулу средней гармонической: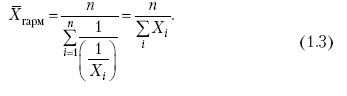

Так, среднее время, необходимое для изготовления единицы продукции, есть средняя гармоническая. Если Х₁ = 1/4 часа, Х₂ = 1/2 часа, Х₃ = 1/3 часа, то средняя гармоническая этих чисел есть: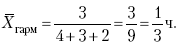

Для расчета средней величины из отношений двух одноименных показателей, например темпов роста, применяется средняя геометрическая, рассчитанная по формуле: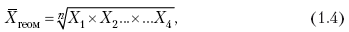

где Х₁? Х₂ … ? … Х₄ – отношение двух одноименных величин, например цепных темпов роста; n – численность совокупности отношений темпов роста.

Рассмотренные средние величины обладают свойством маорантности: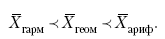

Пусть, например, имеем следующие значения Х (20; 40), тогда рассмотренные ранее виды средних величин будут равны: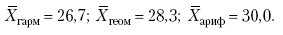

При изучении состава совокупности о типичном размере признака можно судить по так называемым структурным средним – моде и медиане.

Модой называется наиболее часто встречающееся значение признака в совокупности. В интервальных вариационных рядах сначала находят модальный интервал. В найденном модальном интервале мода рассчитывается по формуле: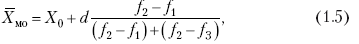

где Х₀ – нижняя граница модального интервала; d – величина интервала; f₁, f₂, f₃ – частоты предмодального, модального и послемодаль-ного интервалов.

Значение моды в интервальном ряду довольно просто можно отыскать на основе графика. Для этого в самом высоком столбце гистограммы от границ двух смежных столбцов проводят две линии. Из точки пересечения этих линий опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс и будет модой (рис. 2).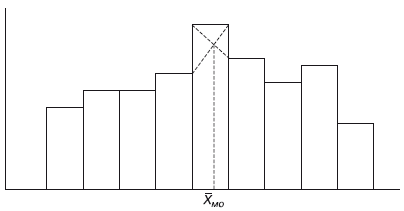

Рис. 2

Для решения практических задач наибольший интерес представляет обычно мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления.

Средняя – величина, типичная для всех единиц однородной совокупности. Мода – тоже типичная величина, но она определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Она имеет большое значение для решения некоторых задач, например для прогнозирования того, какие размеры обуви, одежды должны быть предназначены для массового производства, и т. д.

Медиана – значение признака, находящееся посредине ранжированного ряда. Она указывает на центр распределения единиц совокупности и делит ее на две равные части.

Медиана является лучшей характеристикой центральной тенденции, когда границы крайних интервалов открыты. Медиана является более приемлемой характеристикой уровня распределения и в том случае, если в ряду распределения имеются чрезмерно большие или чрезмерно малые значения, которые оказывают сильное влияние на среднюю величину, а на медиану – нет. Медиана, кроме того, обладает свойством линейного минимума: сумма абсолютных значений отклонений величины признака у всех единиц совокупности от медианы минимальная, т. е.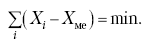

Это свойство имеет большое значение для решения некоторых практических задач – например, для расчета самого короткого из всех возможных расстояний для разных видов транспорта, для размещения станций техобслуживания таким образом, чтобы расстояние до всех обслуживаемых данной станцией машин было минимальным, и т. п.

При отыскании медианы сначала определяется ее порядковый номер в ряду распределения:

Далее, соответственно порядковому номеру, по накопленным частотам ряда находят саму медиану. В дискретном ряду – без всякого расчета, а в интервальном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором путем простейшего приема интерполяции определяется уже значение медианы. Расчет медианы осуществляется по формуле: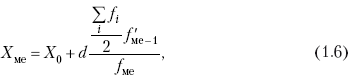

где Х₀ – нижняя граница медианного интервала; d – величина интервала; f _ ₁ – частота, накопленная до медианного интервала; f – частота медианного интервала.

Рассчитаем среднюю величину, моду и медиану на примере интервального распределения. Данные приведены в табл. 2.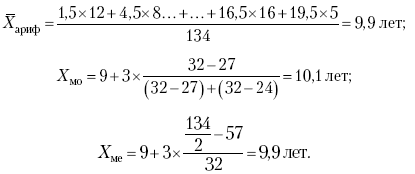

Таким образом, в качестве центра распределения могут быть использованы различные показатели: средняя величина, мода и медиана,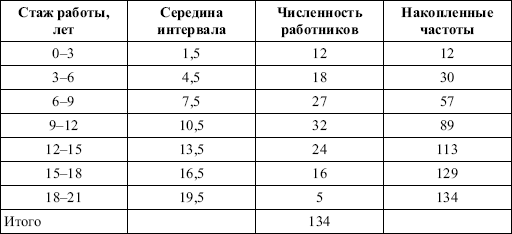

и каждая из этих характеристик имеет свои особенности. Так, для средней величины характерно то, что все отклонения от нее отдельных значений признака взаимно погашаются, т. е.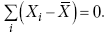

Для медианы характерно то, что сумма отклонений индивидуальных значений признака от нее (без учета знаков) является минимальной. Мода же характеризует наиболее часто встречающееся значение признака. Поэтому в зависимости от того, какая из особенностей интересует исследователя, и должна выбираться одна из рассмотренных характеристик. В отдельных случаях рассчитываются все характеристики.

Их сравнение и выявление соотношений между ними помогает выяснить особенности распределения того или иного вариационного ряда. Так, в симметричных рядах, как в нашем случае, все три характеристики (средняя, мода и медиана) примерно совпадают. Чем больше расхождение между модой и средней величиной, тем более асимметричен ряд. Установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней арифметической: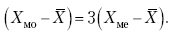

Это соотношение можно использовать для определения одного показателя по двум известным. Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.

Статистическое описание совокупности было бы неполным, если ограничиться лишь показателями центральной тенденции, т. е. средними величинами, модой и медианой, которые являются равнодействующими ряда изменяющихся значений признака. В одних случаях значение признака концентрируется возле некоторого центра очень тесно, в других случаях наблюдается значительное рассеивание, хотя средняя величина может быть одинаковой. В связи с этим средняя величина как показатель центральной тенденции не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака. Хотя отклонения от средней и регулируются общими для всех единиц совокупности причинами, формирующими среднюю, но в то же время они обусловлены и индивидуальными причинами. Например, отклонения производительности труда отдельных рабочих, работающих в одной бригаде, а стало быть, находящихся в одинаковых условиях труда, вызваны не общими условиями и причинами, а индивидуальными обстоятельствами рабочих и их квалификацией, состоянием здоровья, настроением, сообразительностью и т. д. Поэтому изучение отклонений от средней их размеров и закономерности распределения представляет большой интерес для исследователя. Это важно прежде всего для оценки однородности совокупности, которую характеризует данная средняя величина, так как для качественно однородной совокупности характерна вариация в определенных границах. Стало быть, чем меньше вариация, тем качественно однороднее совокупность, тем типичнее и объективнее средняя величина, характеризующая ее.

Измерение вариации имеет большое значение и для изучения устойчивости изучаемых экономических явлений и процессов. Так, для сельского хозяйства очень важно не только получить среднюю урожайность сельскохозяйственных культур, но и обеспечить ее устойчивость во времени и пространстве, а для этого надо научиться рассчитывать показатели устойчивости, научиться измерять вариацию изучаемых явлений ? ? 1,25а.

Для оценки вариации признака статистика знает и использует несколько показателей. Простейшим из них является размах вариации, рассчитываемый по формуле: X_max – X_min, т. е. как разность между максимальным и минимальным значением признака. Однако этот показатель далеко не совершенен, так как при его построении участвуют лишь крайние значения признака, которые могут быть случайными.

Более точно можно определить вариацию признака при помощи показателя, учитывающего отклонения всех значений признака от средней. Это так называемые абсолютные показатели: среднее линейное отклонение а и среднее квадратическое отклонение ?. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений отдельных значений признака от средней величины. Но сумма отклонений от средней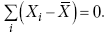

 всегда равна нулю (одно из свойств средней величины), поэтому для расчета среднего линейного отклонения суммируют абсолютные отклонения без учета его знака:

Среднее квадратическое отклонение также может быть простое и взвешенное: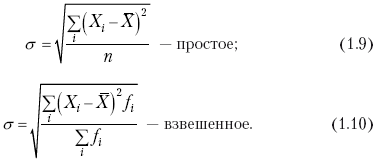

Среднее квадратическое отклонение является наиболее распространенным показателем вариации, оно несколько больше среднего линейного отклонения. Установлено, что в симметричных или умеренно асимметричных распределениях соотношение между ними можно записать в виде:

? ? 1,25а.

Следует иметь также в виду, что среднее линейное отклонение будет минимальным, если оно рассчитано от медианы, т. е.: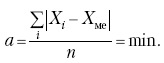

Среднее квадратическое отклонение минимально при вычислении его от средней арифметической, это же относится и к дисперсии, которая представляет собой квадрат среднего квадратического отклонения.

Дисперсия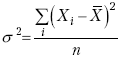 

 широко применяется в дисперсионном анализе, но не как мера вариации, так как ее размерность не соответствует размерности признака.

Содержание среднего квадратического отклонения то же, что и среднего линейного отклонения: т. е. чем меньше а и? тем однороднее совокупность, тем типичнее (объективнее) средняя величина, тем устойчивее явление и процесс.

Рассмотрим вычисление среднего линейного и среднего квадрати-ческого отклонения на примере данных, приведенных в табл. 3.

Таблица 3.

Анализ времени обработки деталей рабочими двух бригад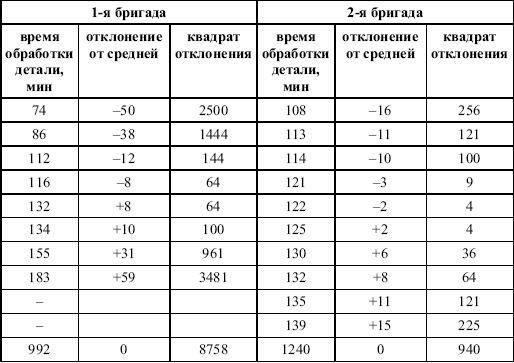

Средняя величина времени обработки детали составляет в обеих бригадах 124 мин. Для первой бригады Х₁ =992/8 = 124ми н. и для второй – Х₂ = 1240/10 = 124 мин.

Медианные значения также одинаковы в обеих бригадах. Так, для первой бригады Хме = (116+132)/2 = 124 мин. Для второй бригады – Хме = (122+126)/2 + 124 мин

Модальные значения в данном случае не могут быть определены, так как каждое из значений признаков не повторяется.

Исходя из полученных результатов, можно сделать вывод, что обе совокупности характеризуются одинаковыми показателями центра распределения, но они могут отличаться по характеру рассеяния отдельных значений признака вокруг этих центров.

Для характеристики рассеяния рассчитаем среднее линейное отклонение. Для первой бригады:

Сопоставление среднего линейного и среднего квадратического отклонений говорит о том, что вариации времени обработки деталей в первой бригаде значительно выше, чем во второй бригаде.

Следует также отметить, что среднее квадратическое отклонение в обоих случаях несколько больше, чем среднее линейное отклонение:

?₁ = 1,22а₁;

?₂ = 1,20а₂.

Это говорит о том, что мы имеем дело с умеренно асимметричным распределением.

Рассмотренные показатели вариации (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение) дают возможность сравнить степень однородности нескольких совокупностей, но в отношении лишь одного признака, поскольку это именованные величины, имеющие единицы измерения те же, что и сам признак.

Однако часто исследователю приходится сравнивать вариации различных признаков, а стало быть, эти показатели вариации не могут быть использованы.

Для характеристики вариации различных признаков рассчитывают относительные показатели вариации, приведенные к одному основанию, т. е. выраженные в процентах (доли размаха вариации, среднего линейного отклонения и среднего квадратического отклонения) от средней величины изучаемого признака.

Это так называемые коэффициент осцилляции, относительное отклонение и коэффициент вариации.

Коэффициент осцилляции рассчитывается по формуле: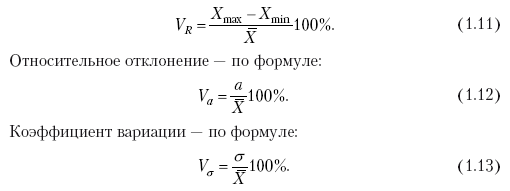

В нашем примере эти показатели составляют:

Все рассчитанные относительные показатели вариации свидетельствуют также о более сильной вариации времени обработки деталей рабочими первой бригады по сравнению со второй, где среднее время обработки является более объективной, более типичной характеристикой работы данной бригады в целом, т. е. вторая бригада как совокупность более однородна.

Относительные показатели вариации, как уже было отмечено, позволяют сравнивать степень вариации признаков, имеющих одинаковые единицы измерения, но разные уровни средних. Например, урожайность зерновых культур и картофеля хотя и имеют одинаковые единицы измерения, но по абсолютным показателям вариации этих признаков сравнивать было бы неправильно, так как сами уровни урожайности зерновых и картофеля резко отличаются. Так, например, в регионе среднеквадратическое отклонение составило: по урожайности ржи – 5 центнеров с гектара (ц/га) и по урожайности картофеля – 20 ц/га, а сама урожайность ржи составила 25 ц/га, а картофеля – 200 ц/га. Коэффициент же вариации соответственно равен:

Это означает, что по урожайности картофеля совокупность хозяйств данной области более однородна, чем по урожайности ржи, т. е. урожайность картофеля более устойчива, чем урожайность ржи.

Сравнение абсолютных показателей вариации одного и того же признака разных совокупностей иногда приводит к иному выводу, чем при сопоставлении относительных показателей вариации.

Так, если в одной совокупности абсолютный показатель вариации больше, чем в другой, и средний уровень изучаемого признака в ней также значительно больше, чем в другой, то относительный показатель вариации может быть ниже.

Так, например, если среднее квадратическое отклонение урожайности ржи в одном районе составило 5 ц, в другом – 3 ц, а сама средняя урожайность, соответственно, составила 25 и 10 ц/га, то относительные показатели вариации приводят к иному выводу.

Следовательно, рост урожайности, связанный с некоторым повышением абсолютного показателя вариации, может и не снизить ее устойчивости.

Относительные показатели вариации необходимы также и для сравнения вариации различных признаков, имеющих разные единицы измерения, поскольку абсолютные показатели вариации в этом случае не могут быть использованы как мера вариации.

Например, при сравнении вариации урожайности и себестоимости той или иной культуры нельзя использовать абсолютные показатели вариации, так как они будут иметь разные единицы измерения: ц/га и руб. за 1 т. В этом случае целесообразно среднее квадратическое отклонение использовать для расчета так называемого нормированного отклонения:

характеризующее отклонение индивидуальных значений признака от средней (Xi ?X) и приходящееся на единицу среднего квадратического отклонения. Нормированное отклонение позволяет сопоставлять между собой отклонения, выраженные в различных единицах измерения. Практически нормированные отклонения изменяются в пределах от 0 до 3.

Однако в совокупности могут встречаться отдельные единицы, у которых t > 3. Это будет свидетельствовать о неоднородности совокупности, и такие единицы совокупности целесообразно исключить как аномальные, нетипичные для данной совокупности.

Если совокупность мала (3 ? n ? 8), то однородность совокупности, т. е. проверку годности первичных данных, можно осуществить следующим образом. Вычисляют показатель, характеризующий отношение разности между сомнительным и соседним значениями ранжированного в порядке возрастания ряда к разности между крайними значениями, т. е.:

если вызывает сомнение первое в ряду значение признака, и:

если вызывает сомнение последнее в ряду значение признака.

Вычисленную величину Q сопоставляют с табличным ее значением для данного числа наблюдений и уровня вероятности. Если Q_ф > Q_табл, то сомнительное значение следует исключить из обработки. Если же Q_ф < Q_табл, то сомнительное значение не отбрасывается. Рассмотрим эту методику на примере.

Допустим, получены следующие результаты содержания золы в образцах корма в процентах: 2,25; 2,19; 2,11; 2,38; 2,32 и 3,21.

Располагаем данные анализа в порядке возрастания их значений: 2,11; 2,19; 2,25; 2,32; 2,38; 3,21.

Вычисляем: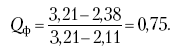

Далее находим Q_табл для n = 6 и вероятности p = 0,99 (табл. 4).

Таблица 4. Значения Q в зависимости от степени надежности (p)

и общего числа значений признака (n)

Величина Q_табл= 0,70. Следовательно, значение 3,21 должно быть исключено как нетипичное для данной совокупности.

При числе значений признака больше трех (и больше восьми) можно использовать другую методику определения пригодности первичных данных. По всем значениям признака в совокупности сначала рассчитывают среднюю величину (Х) и среднее квадратическое отклонение (?), затем на основании разницы (без учета знака) между максимально отклоняющимся значением (X_max) и средней величиной находят величину критерия R_max по формуле: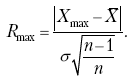

Значение R_max сопоставляют с табличным его значением при данном числе значений признака для вероятности p = 0,99 (табл. 5).

Если R_max > R_табл, то сомнительное значение (X) следует исключить, если же R_max < R_табл, то значение (X_max) следует принимать в расчет.

При n > 20 показатель R_max ? 3 и условие пригодности имеет вид: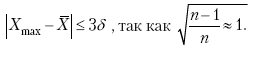

Таблица 5. Значения R_max для степени надежности p = 0,99 в зависимости

от числа единиц совокупности n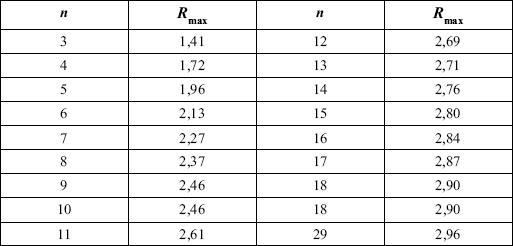

Обратимся к предыдущему примеру и вычислим: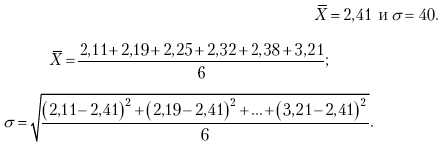

При расчете средней величины и среднего квадратического отклонения используют все значения признака. Затем рассчитываем: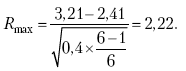

Для n = 6, R_табл _ 2,13; так как 2,22 > 2,13, то сомнительное значение 3,21 необходимо отбросить из статистической обработки. Если сомнение вызывает не одно, а несколько значений, то сначала производят указанные выше расчеты только для одного из них (наиболее отклоняющегося). После его исключения повторяют расчет для следующего сомнительного значения, вычисляя заново X и ?.

При проверке годности данных с использованием любой методики может быть исключено не более одной трети единиц совокупности.

Если исключению подлежит более одной трети всех единиц совокупности, то данная совокупность считается неоднородной.

При изучении экономических явлений статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупностей. Величины признаков варьируют под воздействием различных причин и условий. Чем разнообразнее условия, влияющие на размер признака, тем больше его вариация.

Рассмотренные показатели центральной тенденции и показатели вариации представляют собой частные случаи некоторой единой системы статистических характеристик распределения. Такая единая система характеристик может быть представлена моментами статистического распределения. Если при вычислении моментов за произвольную постоянную принимается средняя арифметическая, то такие моменты называются центральными.

Общая формула центральных моментов k-го порядка имеет вид: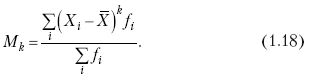

Иначе говоря, центральные моменты k-го порядка представляют собой среднюю арифметическую из k – x степеней отклонений значений признака от средней арифметической.

1. Центральный момент нулевого порядка равен единице при k = 0: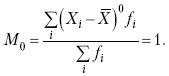

2. Центральный момент первого порядка равен нулю при k = 1: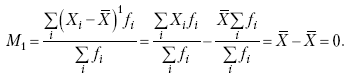

3. Центральный момент второго порядка представляет собой дисперсию данного распределения при k = 2: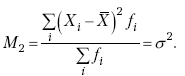

4. Центральный момент третьего порядка имеет вид: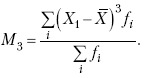

Если распределение симметричное, то нетрудно видеть, что центральный момент третьего порядка равен нулю, так как минусовые отклонения (X_i – X)³ в левой ветви распределения будут уравновешиваться положительными отклонениями в правой части. Такое взаимное погашение отклонений в симметричных рядах распределения сохраняет силу для всех нечетных центральных моментов.

Конец ознакомительного фрагмента. Полный текст доступен на www.litres.ru