Итак, вы решили играть самостоятельно. Вы выбрали стиль игры в соответствии с вашими возможностями, намерениями и характером, а также определили сумму для покупки акций. Вы выбрали брокера и, подписав с ним кабальный договор о том, что вы и только вы будете во всем виноваты, если проиграете, перевели деньги на ваш счет в брокерской фирме. Что дальше? Вы открываете страницы газеты с описанием биржевых курсов и видите списки тысяч компаний, акции которых растут или падают и с первого взгляда не подчиняются никаким законам. Действительно, есть ли законы, определяющие поведение акций? Чем отличается игра на бирже от покупки лотерейных билетов, игры в казино или на скачках? Можно ли найти акции, которые будут расти с большей вероятностью, чем падать, или это все игра случая?

Читая газеты, вы можете встретить забавные рассказы о том, как удачные акции были выбраны курицей, которая клевала зерно, рассыпанное на страницах газет с биржевыми курсами (на какой строчке клюнула — те акции и покупать), собакой, бегавшей по газетам, обезьяной и другими подобными «аналитиками» рынка акций. Выбор этих «аналитиков» любят сравнивать с выбором профессионалов, подчеркивая, что иногда профессионалы оказывались позади.

Так, может быть, книгу на этом и завершить? Вы уже знаете, что такое акции и биржа, как выбрать брокера и как покупать акции. Остается только приобрести лук со стрелами, развесить на стене страницы The Wall Street Journal, завязать глаза и начать стрельбу: стрелы укажут компании, акции которых надо купить. Поскольку рынок в среднем растет, подождав несколько лет, вы скорее всего получите прибыль. Как ни странно, такой метод имеет право на существование, и после такой стрельбы вы можете заработать неплохие деньги.

Однако не надо забывать, что хотя цены акций в среднем растут, но акции каждой отдельной компании вполне могут и падать. Существуют сотни примеров, когда акции, стоившие десятки долларов, падали до нескольких центов. Если просмотреть графики зависимости цен акций различных компаний от времени, то может сложиться впечатление, что на коротком промежутке времени (месяцы или год) движение цен совершенно случайно. Что произойдет с акциями завтра, не зависит от того, что было с ними сегодня, вчера и т.д. Вероятности падения или роста цены на следующий день представляются практически равными. Если это так, то поведение цены акций — это случайный процесс, и игра на бирже мало отличается от игры в казино: полный хаос и все решает случай. К тому же, покупая акции, вы платите комиссионные брокеру и дополнительно теряете деньги на разнице цен покупки и продажи. В таком случае, даже если вероятность выигрыша и проигрыша одинакова, то в среднем вы проиграете за счет указанных затрат.

А может быть, можно получить прибыль и из хаоса, даже если цены акций ведут себя абсолютно случайным образом? Для подобных процессов разработаны специальные методы, и соответствующий раздел математики называется теорией случайных блужданий, в рамках которой динамика цены акций рассматривается как случайное блуждание точки по оси цен. Эта теория получила широкое распространение среди теоретиков биржи в 50-х годах, когда расчеты на первых компьютерах показали ее соответствие поведению рынка акций. Последующее, более глубокое изучение биржевых процессов выявило ее недостаточность, но об этом мы расскажем позже. Пока же ознакомимся с методами этой теории, которые до сих пор используются аналитиками. Для этого попробуем придумать стратегию биржевой игры, дающую прибыль при условии, что цена выбранных акций подчиняется законам случайных блужданий, т.е. вероятности роста или падения цены равны и не зависят от прошлого поведения акций. Будем рассматривать только изменение цен акций, пренебрегая брокерскими комиссионными и другими затратами.

Простейшая стратегия — это купить акции и, если они вырастут в цене на L долларов, — продать. Если изменение цены случайно, то рано или поздно цена коснется установленного вами предела и вы получите прибыль. В теории случайных блужданий есть теорема, что если объект (в нашем случае цена акций) начинает случайные блуждания по оси х из точки X₀, to какую бы точку X мы ни выбрали, рано или поздно объект попадет в точку X с вероятностью, равной единице. В случае игры на бирже X₀ — цена акций при покупке, X — цена акций при продаже и разница

будет вашей прибылью. Иными словами, надо купить акции и ждать, пока образуется прибыль. К сожалению, как будет показано, средняя прибыль от такой игры равна нулю, т.е. эта стратегия неперспективна. В ней, помимо практической невозможности ожидать желаемого бесконечно долго, есть еще и теоретическая тонкость: если цена акций упадет до нуля, то это означает банкротство компании, и процесс ожидания прибыли прервется. Российские инвесторы (да и не только российские) хорошо представляют такую ситуацию. Иными словами, цена акций может блуждать между нулем и числом X. Как только цена коснется одной из этих границ, процесс блуждания окончится, и можно начать подсчет прибылей или убытков. Возможную прибыль мы обозначим буквой L, а возможные убытки обозначим буквой S. В рассматриваемом случае S = Х₀, т. е. возможные потери равны первоначальной стоимости акции. Чтобы лучше представить такой метод игры на бирже, мы приведем рисунок, где указаны наши обозначения.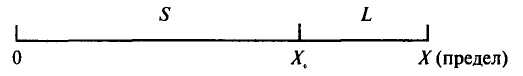

Предположим, что цена акций меняется каждый день, вырастая или падая на один доллар с равной вероятностью. В этом случае, можно доказать, что вероятность касания точки X раньше, чем точки 0, т.е. вероятность получения прибыли, равна

а вероятность касания точки 0 раньше, чем точки X, т.е. вероятность проигрыша, равна

Средняя прибыль G (в долларах) при таком описании биржевой игры и такой стратегии будет равна вероятности выигрыша, умноженной на величину выигрыша, за вычетом произведения величины проигрыша на вероятность проигрыша. Математически это можно записать в виде

а подставив значения P(L) и P(S), получим G = 0. Как видите, средняя прибыль от такой игры действительно равна нулю. Часть ваших акций коснется точки X, и вы получите прибыль, а часть акций погибнет, и у вас будут потери. (Если вы инвестируете все свои средства в акции одной компании, то P(S) — вероятность полной потери капитала.) Конечно, в зависимости от величин S и L реальные результаты игры за ограниченные промежутки времени будут разными. Чем меньше ваш начальный капитал (это величина, сопоставимая с S или Х₀) и чем больше вы хотите заработать, тем больше вероятность вашего полного разорения. С другой стороны, если ваш капитал велик, а цель достаточно скромна, то ваш шанс на выигрыш вполне реален. Это простейший пример, показывающий, что меньшая прибыль всегда связана с меньшим риском. Однако надо помнить, что при длительном использовании такой стратегии в любом случае рано или поздно можно потерять все, так как вероятность проигрыша P(S) отлична от нуля.

Таким образом, здесь нужно долго ждать, и всегда есть вероятность проиграть все инвестированные деньги. Естественно, вам такая стратегия не понравилась, хотя многие новички, сами того не подозревая, пользуются именно ею. Инициативный читатель, наверное, уже готов предложить другую, более продуктивную стратегию, и мы попробуем рассмотреть иные варианты.

Действительно, совершенно бесспорны две посылки: нельзя допускать потерю всех денег, даже с маленькой вероятностью такого события, и нельзя ограничивать себя выигрышем небольшой суммы. Стратегия, объединяющая оба эти требования, выглядит следующим образом. Вы покупаете акции по цене Хо. Если цена падает на величину S, то вы продаете акции с потерей S долларов. Если цена увеличивается, вы не продаете акции сразу, а ждете, когда они вырастут более значительно. Ваша возможная прибыль L может быть очень большой (например, вы будете ждать пока цена акций удвоится). Графически схема такой стратегии выглядит следующим образом.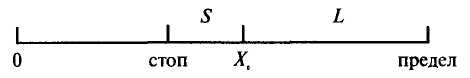

Математически эта задача полностью эквивалентна предыдущей. Средняя прибыль G также равна нулю с той только разницей, что при такой стратегии S < L и вероятность проигрыша больше, чем вероятность выигрыша. Но сами проигрыши небольшие, а выигрыши, хоть и редки, но значительны. В среднем же по разным акциям за достаточный промежуток времени ваш результат все равно будет нулевым (опять без учета комиссионных и разницы между покупной и продажной ценой акций).

Можно придумать и другие способы игры. Например, во второй схеме можно при выигрыше L долларов не продавать акции, а переместить «стоп» вправо, чтобы гарантировать сохранение части выигрыша и иметь шанс увеличить его еще больше в случае дальнейшего роста акций. Не анализируя подробно эту стратегию, отметим, что и в этом случае выигрыш в среднем будет равен нулю. Ни одна стратегия не дает иного результата: если цены акций изменяются в соответствии с законом случайных блужданий, то игра на бирже мало чем отличается от игры в казино. Большой выигрыш приносит лишь «госпожа удача», и остается только надежда на средний рост акций вместе с рынком в целом, который составляет около 10 — 12% в год. Это главный вывод университетских теоретиков, пропагандирующих теорию эффективного рынка акций, не помнящего истории и мгновенно реагирующего на все экономические новости. А если рынок не помнит истории, то изменение цен акций случайно.

У инвестора есть еще один коварный враг. Во всех проведенных расчетах нулевой результат описанных стратегий был получен, если перед началом очередной игры вы каждый раз имели некоторую фиксированную сумму. Так, если в начальный момент у вас было 100 долларов и вы проиграли 20 долларов, т.е. 20%, то для следующей покупки акций вы должны добавить 20 долларов и купить акции опять на 100 долларов. Если вы выиграли 20 долларов и у вас стало 120 долларов, то вы должны убрать «лишние» деньги в ящик и купить акции снова на 100 долларов.

А если у вас есть капитал 100 долларов, который вы решили полностью использовать для игры на бирже, и, не желая ничего отнимать, не можете ничего и добавить? Что произойдет, если при покупке акций вы будете каждый раз использовать все имеющиеся деньги? Допустим, для простоты, что вы используете стратегию, которая позволяет вам с равной вероятностью выигрывать 20% или проигрывать те же 20%. В случае выигрыша ваши 100 долларов превращаются в 120 долларов:

Если при следующей попытке вы проиграете 20%, то в результате у вас окажется не 100, а 96 долларов:

Таким образом, после одного выигрыша и одного проигрыша ваш капитал станет меньше начального. При продолжении игры ваши 96 долларов после еще одного выигрыша и проигрыша превратятся в 92,16 доллара, а после 10 «циклов» у вас останется только 44,2 доллара, т.е. меньше половины начального капитала! Этот пример показывает, что кажущаяся нейтральность такой игры очень коварна. Вкладывая в игру весь капитал, вы постепенно его теряете.

Это очень важная закономерность игры на бирже, и потому рассмотрим ее подробнее. Предположим, что вы играете по описанной схеме, используя для каждого трейда весь наличный капитал (трейдом мы будем называть покупку акций какой-либо компании с их последующей продажей, при игре на понижение трейдом является продажа акций с их последующей покупкой). Для удобства рассуждений введем коэффициент роста К. Если капитал до начала трейда был равен Х₀, а после окончания трейда он стал X, то коэффициент роста равен среднему отношению

т. е. при выбранной стратегии он равен среднему относительному увеличению капитала в результате одного трейда.

С помощью такого коэффициента можно вычислить среднюю прибыль или убыток, которые получаются после N-го трейда. Для этого надо коэффициент К возвести в N-ю степень. Так, если К = 1,05, то после 10 успешных трейдов ваш капитал в среднем увеличится в 1,0510 = 1,63 раза или на 63%.

Предположим, что вы играете на повышение курса акций по рассмотренной ранее схеме. Если цена падает на S долларов, то вы продаете акции с убытком, а если вырастает на L долларов, то вы продаете акции с прибылью. Относительные величины прибыли l и убытка s вычисляются делением на начальный капитал:

Используя методы теории вероятностей, можно показать, что если цена акций меняется по законам случайных блужданий, то

Эта величина при любых значениях J и s всегда меньше единицы, что легко проверить методом подстановки.

Подводя итог, можно повторить, что в случае полного хаоса, если поведение акций описывается законами случайных блужданий, никакая стратегия при длительной игре не может дать прибыль. Более того, неправильная стратегия, связанная с плохим выбором уровня «стопа» S и предела L, на котором инвестор планирует продать акции с прибылью, может привести к быстрому разорению. Брокерские комиссионные и другие накладные расходы еще больше усугубляют ситуацию.

Прочитав эти строки, большинство читателей, вероятно, будут весьма разочарованы: зачем же тратить время на изучение рынка акций, если игра на бирже в принципе приводит к разорению? Автор, однако, просит набраться терпения и не прекращать чтения книги — все не так плохо, как сейчас может показаться. Рассмотренные методы расчетов нам пригодятся — их широко применяют в аналитической работе, так как они дают удобные модели, соответствующие случайному характеру биржевых процессов. Но они не отражают всей сложной природы акций и их движения, в котором есть не только случайности, но и закономерности. Строго говоря, в целом цены акций не подчиняются законам случайных блужданий, и мы будем непрерывно демонстрировать это на протяжении всей книги. Если даже они «случайно блуждают» в течение короткого времени (хотя и в этих случайностях есть свои закономерности), то нужно помнить, что при рассмотрении многолетней динамики средние цены акций растут, т.е. вероятность их роста больше, чем падения. В этом аспекте цены можно рассматривать, как движение водомерок на поверхности реки. Их перемещения относительно поверхности случайны, но все они вместе с рекой в среднем движутся в одном направлении. В таком случае задача инвестора состоит в выборе стратегии, которая позволит удержаться на поверхности как можно дольше, чтобы река унесла цены в нужном направлении.

Если все-таки оставаться в рамках модели случайных блужданий, которая длительное время удовлетворяла теоретиков биржевых процессов, то какая стратегия может считаться оптимальной? Иными словами, какая стратегия дает минимальные средние потери при длительной игре?

Для ответа на этот вопрос проанализируем коэффициент роста К. Как уже говорилось, при случайных блужданиях он всегда меньше единицы, и наша задача — найти стратегию игры, которая максимально приблизит его к единице. Читатели, знакомые с математикой, могут убедиться, что этот коэффициент может быть представлен очень простой формулой: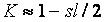

Эта формула приближенная, но она очень хорошо работает в большинстве практически интересных случаев. Из нее легко видеть, что для более долгого «удержания на плаву» необходимо ставить перед собой достаточно скромные цели, не завышая ожидаемые прибыли (величину l), и быстро обрезать потери, стараясь уменьшить величину s.

Обрезание потерь является более важным, так как величина s обычно мала и при «стопе» 5 % (s = 0,05) вы получите значительно лучший результат, чем при «стопе» 15% (s = 0,15), ибо это уменьшит произведение sl в три раза, а изменение величины l с 40 % до 30 % даст относительно меньший эффект.

Другой важный способ увеличения коэффициента роста — это диверсификация, т.е. деление инвестиционного капитала между акциями нескольких компаний. Как вычисляется коэффициент роста в этом случае? Допустим, что вы купили акции n компаний, разделив ваш капитал поровну между ними. После продажи этих акций вы снова поровну делите деньги, вырученные за их продажу, и покупаете акции других n компаний. Предположим, что ваши цели каждый раз идентичны, величины s и l не зависят от выбора компаний и все купленные вами акции ведут себя независимо. Не рассматривая соответствующие расчеты, мы сразу напишем окончательную приближенную формулу. Если разделить капитал на n частей, то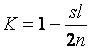

При увеличении n коэффициент роста стремится к единице, значит, диверсификация уменьшает средние потери.

Но подождите радоваться. Если у вас есть 1000 долларов и вы наметите разделить эти деньги между акциями 10 различных компаний по 100 долларов на компанию, то это будет самоубийственным решением. При величине брокерских комиссионных (оплата взимается за покупку или продажу акций одной компании), допустим, 30 долларов вам нужно будет получить 30 долларов или 30% прибыли на акциях каждой компании, чтобы выйти хотя бы с нулевым результатом. Эта задача нереальна даже для профессионалов. Для любого начального капитала Х₀, который имеется в наличии до начала трейда, существует некоторое оптимальное разбиение в зависимости от величины комиссионных. Если обозначить величину комиссионных в долларах через С, то коэффициент роста можно записать в виде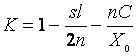

,

при этом максимальный коэффициент роста получается, если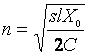

.

Эта формула позволяет вычислить оптимальное число долей, на которые надо разбить начальный капитал для уменьшения потерь. Соблюдение данной формулы может быть не очень строгим — она допускает некоторое варьирование, которое математически связано с пологостью максимума распределения. Для иллюстрации в таблице 5.1 приведены результаты расчетов величин n в случае l = 0,2; s = 0,02; С = 30 долларов.

Таблица 5.1.

Под капиталом мы понимали сумму, доступную для трейдинга, включая деньги на маргинальном счету. Как можно видеть из этой таблицы, если вы располагаете капиталом менее 10000 долларов, то лучше эти деньги вложить в акции одной или двух компаний. Если вы играете на дневных колебаниях курса акций, и соответственно интересуетесь прибылью 1 — 2% (l = 0,01 — 0,02), то нужно сконцентрироваться на покупке акций какой-то одной компании. Если вы инвестируете и ожидаете прибыль порядка 30 — 50% (l = 0,3 — 0,5), то лучше разбить капитал на несколько частей.

Специалисты по теории вероятностей могут продолжить начатую нами работу. Можно, например, рассмотреть задачу о случайном блуждании цены акций в предположении, что она не будет касаться нуля, а будет от него отражаться. То есть предположить, что вероятность разорения компании очень мала, что имеет смысл для компаний, представленных на нью-йоркской бирже.

Но мы не будем этим заниматься. Все эти задачи имеют только академический интерес, поскольку на бирже работают другие законы: изменение цен акций не является совершенно случайным. Что же изменится в наших рекомендациях, если предположить, что цены акций меняются не случайно? Почему они могут меняться не случайно? К ответу на эти вопросы мы сейчас и приступим.

В этом разделе мы немного отдохнем от математики и рассмотрим некую гипотетическую ситуацию.

Представьте, что вы пришли в офис своего приятеля Майкла президента компании Michael & Co., которая производит замечательные авторучки и выглядит довольно успешной. И вы с порога заявляете, что, по вашему мнению, цены акций компании Майкла, как и всех других компаний, подчиняются законам случайных блужданий. Какова будет реакция Майкла?

Боюсь, что он выдворит вас из кабинета и посоветует больше никогда не приходить. И это понятно: Майкл посвятил всю свою жизнь борьбе за успех своей компании, у него нет долгов, много наличного капитала. Компания начала производство авторучек со специальными чернилами, которые легко удаляются с бумаги специальным карандашом, продающимся в комплекте с авторучкой. Продажи растут, прибыли за последний год выросли на 50%. А тут какой-то умник-теоретик заявляет о случайных блужданиях. Для чего тогда Майклу и его команде вообще ходить на работу?

Давайте лучше спросим у Майкла, как он оценивает вероятность роста своих акций в текущем году. Возможно, он ответит — 70%. Почему не 100%? А потому — как расскажет вам Майкл — что этот стирающий карандаш немного попахивает, а конкурент Джим из компании James & Со уже нанял трех «бездельников» из местного университета, которые сидят днями и ночами, доказывая, что от этого карандаша могут возникнуть семнадцать болезней, одна страшнее другой. Но Майкл тоже не промах: он нанял трех толковых ребят, которые работают над этим карандашом и обильно сдабривают его парфюмерией. Если дело так пойдет и дальше, то к концу квартала в продаже появится уже другой карандаш и исследования Джима ничего не будут значить — у Майкла новый продукт. Короче говоря, вероятность роста акций — 70% и ни грамма меньше.

Джим работает в небоскребе напротив, и вы отправляетесь к нему. Его офис явно требует ремонта, и хозяин настроен менее оптимистично. На вопрос о вероятности роста его акций, он грустно говорит, что больше 30% он не даст, потому что в конце квартала ему надо рассчитываться с банком, а для этого придется занимать деньги у другого банка, который требует за заем сумасшедшие проценты. Да еще этот проклятый Майкл купил все время на телевидении, рекламируя свои стираемые чернила, и победить такого конкурента будет не просто. У него только надежда на жуткий запах стирающего карандаша Майкла и на свою лабораторию, которая придумала чернила, светящиеся в темноте и не размываемые водой. Их могут использовать водолазы, спелеологи и еще уйма всякого люда романтических профессий. Это вселяет надежду, но больше 30% вероятности роста его акций он не даст.

Вот тебе и на! Весь рынок случайно блуждает туда сюда, как пьяный муравей по проволоке, а вы за час нашли две компании, акции которых явно не будут случайно блуждать, а пойдут наверх или вниз совсем по другим законам. Жалко, что вероятности не равны 100%: тогда вы сумели бы сделать хорошие деньги на этих акциях, играя на одних на повышение, а на вторых на понижение. И все было бы чудесно, но сейчас... Все знают о трудностях Джима и постарались избавиться от его акций еще три месяца тому назад и теперь они очень дешевы. А вдруг светящиеся чернила станут популярны? Тогда эти акции полетят вверх, как птички, выпущенные из клетки. Может, стоит рискнуть — ведь 30% вероятности не так уж мало. Акции Майкла стоят безумно дорого. Все верят в успех его компании, и каждый уважающий себя инвестиционный фонд, уже купив его акции, готов купить еще, если успех со стирающим карандашом будет развиваться.

Что же делать? Можно ли здесь получить прибыль?

Эта длинная история приводит нас к мысли, что на рынке акций не все регулируется теорией вероятности и «случайные блуждания» не совсем случайны. На акциях, цены которых случайно блуждают, в среднем сделать прибыль нельзя, как это было показано в предыдущем разделе, а с акциями Джима и Майкла прибыль сделать можно.

Представьте, что вы инвестировали равные суммы в акции этих двух компаний и стали использовать вторую схему инвестирования, описанную в предыдущем разделе. Вы поставили «стоп», чтобы обрезать потери в случае неудачи, и ждете хорошей прибыли от акций, которые не коснутся «стопа», а пойдут наверх. Если уровень «стопа» равен 5%, то потери от акций Джима (если они упадут) составят 2,5% от вашего капитала, так как на эти акции вы потратили только половину денег. Если акции Майкла вырастут на 30%, ваша прибыль от них составит 15% от вашего капитала. В итоге это даст 12,5%, что явно больше нуля, который вы получили бы от двух компаний, акции которых «случайно блуждали» на протяжении этого года. При правильной стратегии инвестирования плюс и минус не равняются нулю!

Чтобы лучше представлять картину изменения цен акций на реальном рынке, вообразите ледяную гору и тысячи жуков, пытающихся подниматься по ее склонам. Цена конкретных акций — это высота, на которой находится отдельный жук. Ветер, дующий по направлению к вершине, это общий подъем рынка, который в среднем помогает всем жукам подняться на новую высоту. Иногда ветер меняет направление, и жуки начинают дружно сползать вниз — это падающий рынок. Чаще ветер дует от подножия к вершине, но тем не менее отдельные жуки периодически теряют равновесие и скатываются вниз, к тому же более сильные постоянно сталкивают слабых — это конкуренция. Все они очень разные. На кого-то навешен тяжелый груз долговых обязательств, и таким очень трудно карабкаться наверх. Очень тяжелые жуки ползут медленно и степенно, осторожно выбирая безопасный путь, — это гиганты рынка типа IBM, Coca-Cola и др. Маленькие резвые жучки бегут наверх быстро, но, поскользнувшись, так же быстро откатываются назад — это молодые развивающиеся компании.

Жуки делятся на группы (отрасли), каждая из которых имеет свой маршрут. У одних он проходит по пологому склону, и выход на новую высоту занимает много времени. Для таких групп (коммунальное обслуживание, финансы и т. п.) очень важно направление и сила ветра. Другие группы ползут по почти отвесной стене, подъем идет быстро, но связан с большими опасностями: часто срываются не только отдельные жуки, но и целые группы. Это «жуки» из компьютерной, биотехнологической и других подобных отраслей. Задача инвестора — найти жука, который находится на оптимальном маршруте, может выстоять перед встречным ветром и достаточно силен, чтобы не быть затоптанным другими. Иными словами нужно найти жука, у которого вероятность подняться на новую высоту больше, чем вероятность скатиться вниз. Но можно ли это сделать?

Посмотрим, что говорит по этому поводу сухой язык математики. Если предположить, что цены акций меняются в соответствии с законами полного хаоса, то разность цен акций за определенное количество дней должна быть распределена по закону Гаусса — вероятность найти определенную разность цен должна описываться колоколообразной гауссовой кривой. Вычисления целого ряда авторов показали, что «хвосты» реальных распределений лежат выше теоретических значений. Это означает, что очень большие и очень малые изменения цен встречаются чаще, чем им положено. Есть акции, которые меняются быстрее (или более стабильно), чем им разрешает закон случайных блужданий, а значит это происходит не случайным образом. Именно это было ясно на примере жуков «альпинистов»: есть сильные и есть слабые жуки, у которых вероятности подняться и опуститься отнюдь не равны. Точно так же есть сильные и слабые компании.

А теперь главный вопрос: можно ли прогнозировать вероятности роста или падения курса акций? И главный ответ: да, можно! Далее будут приведены результаты статистического анализа рынка акций за последние 40 лет, которые показывают, что изучение финансовых показателей компаний дает достаточные основания для оценки шансов их роста или падения курса их акций. Такой анализ далеко не однозначен и позволяет говорить только о вероятностном прогнозе движения акций, но и этого достаточно, чтобы на протяжении длительного времени получать от инвестирования большую прибыль, чем только за счет среднего роста рынка или с помощью среднего инвестиционного фонда.

Как проводить такой анализ, мы расскажем позднее, детальнее ознакомившись с финансовыми показателями компаний. Пока же обсудим некоторые подробности оптимальных стратегий игры на бирже в случае, когда блуждания цен акций не случайны, т.е. вероятности их роста и падения различны. Мы постараемся четко сформулировать основные выводы и надеемся, что они помогут начинающему инвестору выбрать такую стратегию, которая даст максимальную прибыль при допустимом для него риске.

Рассмотрим нашу старую модель изменения цены акций. Пусть каждый день цена меняется на один доллар, но вероятность роста (обозначим ее р) не равна вероятности падения (обозначим ее q). Очевидно, что

Предположим, что вы используете стратегию инвестирования, при которой потери обрезаются при падения цены на S долларов (на этой цене стоит «стоп») и акции продаются с прибылью L долларов, если цена достигла этого предела. В теории случайных блужданий (желающим детальнее ознакомиться с этими вопросами мы рекомендуем книги В. Феллера) доказывается, что P(S) — вероятность того, что цена коснется точки S раньше, чем точки L, т.е. вероятность проигрыша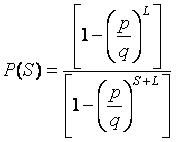

P(L) — вероятность того, что цена коснется точки L раньше, чем точки S, т.е. вероятность выигрыша

При такой стратегии ваша средняя прибыль G (в долларах)

Анализ этих уравнений показывает, что вариант с различными вероятностями роста и падения цены, когда р q, качественно отличается от варианта совершенно случайных блужданий, когда р = q. Средняя прибыль равна нулю лишь тогда, когда р = q. Если р q, средняя прибыль отлична от нуля и, кроме того, вероятности выигрыша или проигрыша начинают зависеть не только от отношения L/S, но и от абсолютных величин L и S. Эти принципиальные моменты, важные для биржевой игры, необходимо рассмотреть подробнее.

Представьте, что вы купили акции по цене 100 долларов за штуку. Данные акции довольно активны, и их цена меняется в среднем на один доллар в день. Вы решаете, что акции могут вырасти до 104 долларов (L = 4), и ставите мысленный предел 104 доллара, когда вы их продадите с прибылью 4%. Для предотвращения больших потерь вы ставите «стоп» на 99 долларов (S = 1), и ваши максимальные потери будут 1 %. Какова вероятность выигрыша Р (L) и какова средняя ожидаемая прибыль G?

Ответ будет зависеть от вероятности р, т.е. от вероятности того, что акции вырастут в цене в течение одного дня. Если р = 0,5 (50% — «случайные блуждания»), то ответ на эти вопросы можно найти в начале данной главы: вероятность выигрыша P(L) = 20 % и средняя ожидаемая прибыль будет равна нулю. А что произойдет, если вероятность р будет равна 0,7 или 0,3? Результаты расчета приведены в таблице 5.2.

Вероятности выигрыша в обоих случаях меньше 60%, хотя средняя прибыль при р = 0,7 положительна и составляет 1,9 долларов, т. е. почти 2%. Это больше, чем средние потери от покупки акций с р = 0,3. Если бы вы купили акции двух компаний с р = 0,7 и с р = 0,3, вложив по 50 % капитала в каждую из них, то средняя прибыль от такого инвестирования составила бы (1,9 - 0,9)/2 = 0,5 % от начального капитала (деление на 2 возникло не из-за усреднения, а потому, что капитал был разделен между двумя компаниями).

Таблииа 5.2.

Теперь рассмотрим другую важную задачу. Представьте, что вы занимаетесь трейдингом и ваш начальный капитал составляет 100 долларов. Вы покупаете и продаете акции различных компаний, среди которых равновероятно встречаются компании с р = 0,7 и р = 0,3. При этом все деньги, вырученные за продажу очередных акций, вы тратите на покупку следующих, ничего не добавляя и не откладывая. Можно ли получить прибыль при такой стратегии игры? Эта задача близка к методу выбора акций при помощи лука со стрелами, когда вероятности выбора «хороших» и «плохих» компаний практически одинаковы. В таком случае надежду можно возлагать лишь на то, что обрезание потерь «стопами» поможет быстро избавиться от плохих компаний и получить прибыль от хороших. Условия выберем прежние: «стоп» составляет 1 % от стоимости акций, и вы продаете акции, получив 4% прибыли.

Анализ данной задачи аналогичен тому, который был проведен в конце раздела 5.1. Коэффициент роста К вычисляется следующим образом:

т. е. он больше единицы, и средняя прибыль на один трейд составляет около 0,8% (коэффициенты ? в показателях степени возникли из-за равной вероятности выбора компаний с р = 0,3 и р = 0,7). Через 10 трейдов начальный капитал увеличится в среднем в 1,00810 = 1,083 раз, или на 8%.

Из рассмотренных примеров можно сделать простой вывод: выбирая акции даже случайным образом, можно получить прибыль, если ограничивать потери на случай падения акций, а при их росте дожидаться заметного повышения цены акций. Эта простая истина давно известна на биржах, и мы лишь математически показали, что лежит в ее основе. Но не могут ли рассмотренные модели подсказать оптимальные уровни обрезания потерь и помочь сопоставлению планируемых прибылей с потерями?

Ответ на этот вопрос зависит от распределения вероятностей роста и падения акций. Очевидно, что при растущем рынке практически для всех акций вероятность роста больше, чем вероятность падения. Акции компаний популярной отрасли имеют большую вероятность роста, чем акции других компаний. Опытные инвесторы или трейдеры выбирают акции лучше, чем начинающие, поэтому у выбранных ими акций средние вероятности роста больше 0,5.

Математически это описывается с помощью некоторой функции распределения. Положение максимума этой функции приблизительно совпадает со средней вероятностью роста акций. Учитывая задачу этой книги, мы не будем обсуждать тонкие детали возможных типов распределения, а ограничимся одной простой моделью. Многолетние наблюдения за поведением акций показали, что цена большинства из них колеблется в некоторых пределах, но максимальная вероятность у р, близкого к 0,5. Чем больше р отличается от 0,5, тем реже встречаются такие акции. Наша модель как раз и учтет эту закономерность.

Предположим, что распределение вероятностей роста акций максимально при р = 0,5 и равно нулю при р = 0 и при р = 1. Иными словами, число акций, имеющих 50%-ную вероятность роста за день, максимально, а акций, которые будут падать или расти со 100%-ной вероятностью, не существуют. Между этими значениями функцию распределения для простоты представим линейной, и распределение будет иметь форму равнобедренного треугольника. Если рынок растет, то центр этого треугольника будет смещаться вправо, что означает, что число акций с р > 0,5 превышает число акций с р < 0,5. Треугольная форма распределения остается неизменной, а происходит небольшое его смещение вправо. При падающем рынке число падающих акций превосходит число растущих акций, и наш треугольник будет смещаться влево. Мы проведем расчеты для трех положений центра треугольника — в точках 0,4; 0,5 и 0,6. Эта же модель соответствовать и разным вероятностям выбора «хороших» акций новичками (центр распределения в точке 0,4), средним трейдером или инвестором (центр в точке 0,5) и опытными игроками (центр в точке 0,6).

На основании предложенной модели распределений можно решать практически важную задачу: определить зависимость коэффициента роста К от значений S и L при различных распределениях. Мы рассчитали величины К при разных значениях S и L для трех различных состояний рынка. Полученные результаты приведены на рисунке 5.1 в виде контурных графиков. Точечная линия, проведенная через максимальные значения К указывает на оптимальные значения «стопов» S для различных значений L.

Анализируя данные графики, можно сделать очень важные выводы. Главный из них состоит в том, что если у акций существует распределение вероятностей их роста, то трейдер или инвестор может получить положительную прибыль, опираясь на адекватную стратегию, т.е. разумно планируя ожидаемую прибыль L и правильно расставляя «стопы» S.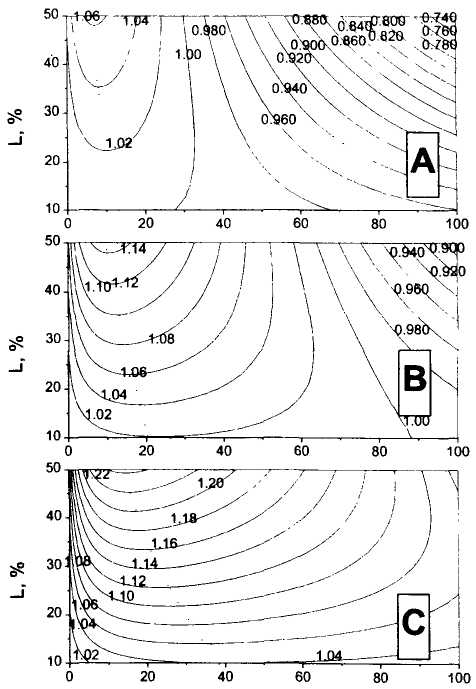

Для падающего рынка при игре на повышение «стопы» необходимо ставить как можно ближе к текущей цене акций. Так. например, если вы решили, что акции могут вырасти на 20%, после чего вы их продадите, то «стоп» нужно ставить на уровне 10% от 20% — на уровне 2% от первоначальной цены. При нейтральном рынке «стопы» могут быть немного отодвинуты. При растущем рынке «стопы» могут составлять до 40% от величины намеченной прибыли. Таким образом, если L = 20 %, то стоп может стоять на уровне 8 % от начальной цены акций. Стратегия, в которой «стоп» S равен по величине планируемой прибыли L, самоубийственна: так, при S = L = 50% даже при нейтральном рынке трейдер будет терять на каждом трейде около 10% капитала. Трейдинг с большими планируемыми прибылями вообще опасен, здесь особенно важен выбор «стопов»: чем больше L, тем ближе должен быть «стоп» к текущей цене.

Как уже было отмечено, такая же модель описывает и распределение выбора акций биржевыми игроками разной квалификации. Начинающие игроки чаще выбирают неудачные акции, и их единственная возможность сохранить инвестиционный капитал — расстановка очень близких «стопов». Более опытные игроки, которые выбирают акции с большей вероятностью роста, могут позволить себе поставить «стопы» подальше.

Рассмотрим еще некоторые закономерности, сопутствующие покупке акций, у которых вероятность роста р отличается от вероятности падения q. В приведенных ранее примерах мы предполагали, что дневное изменение цены акций равнялось одному доллару. А что изменится, если изменение цены за день будет меньше, например, 0,5 или 0,25 доллара? Как изменятся вероятности выигрыша и проигрыша, средняя прибыль и продолжительность одного трейда? Обозначим изменение цены за день через АХ. Результаты расчетов для различных АХ при фиксированных величинах предела L = 4 и «стопа» S = 1 показаны в таблице 5.3.

Таблица 5.3.

Результаты, как видим, поразительны. При уменьшении изменения цены акций резко вырастают вероятности выигрыша при р = 0,7. При этом величина проигрыша при р = 0,3 остается неизменной, так как она ограничена уровнем «стопа», а выигрыш при р = 0,7 растет, асимптотически стремясь к величине своего предела L = 4. Единственный недостаток в таком случае — не отраженное в таблице резкое увеличение средней продолжительности трейда.

Таким образом, если изменение цены акций происходит более мелкими шагами, то при р > 0,5 вероятность выигрыша и величина прибыли заметно возрастают. Однако в таком случае инвестору надо быть готовым к длительному ожиданию запланированной прибыли.

Есть еще одна интересная закономерность, связанная с уменьшением кванта изменения цены акций. Чтобы выявить ее более четко, проведем вычисление вероятности срабатывания «стопа» при р = 0,4 в случае S = L = 1. Такую ситуацию можно представить в случае длительного роста акций, когда вероятность падения цены уже больше, чем вероятность ее роста. Трейдер хочет попробовать «вытянуть» последний доллар прибыли и пододвигает «стоп» как можно ближе к текущей цене акций. Его решение таково: если цена поднимется еще на доллар, то акции надо продавать. Если же цена упадет на доллар, то акции автоматически будут проданы «на стопе». Какова вероятность P(S), что сработает «стоп»? Ответ можно получить из таблицы 5.4.

Таблица 5.4.

Вывод простой: при «вытягивании» последнего доллара, когда вероятность падения цены уже больше, чем вероятность ее роста, шанс потерять доллар резко возрастает с уменьшением кванта изменения цены акций. Иными словами, если акции выросли в цене до предела, который вы планировали для выхода, а далее изменение цены стало происходить малыми квантами, то лучше продать акции, не испытывая судьбу: вероятность выигрыша очень мала. Здесь уместно привести слова отца бывшего президента США Джона Кеннеди — Джо Кеннеди, который в свое время был известным трейдером на Уолл-стрит. Он сказал: «Только глупец держит (акции), чтобы получить последний доллар».

В этом месте нелишне напомнить о неизменно полезной диверсификации, которая осуществляется разбиением капитала между акциями нескольких компаний. Она эффективна и в данном случае, но только следует иметь в виду, что разбиение капитала, резко уменьшая вероятность потерь, приводит к некоторому уменьшению коэффициента роста.

И еще надо осознавать, что выводы, которые мы сделали на основе анализа различных моделей рынка, относятся к моделям, а не к реальному рынку. Данные модели были рассмотрены не для получения конкретных цифр, которые можно использовать для планирования прибыли или расстановки «стопов», а для иллюстрации общих принципов трейдинга и важности выбора правильной стратегии.

Отметим также, что планируемая прибыль и «стопы» должны выбираться не на основе слепого следования каким-либо принципам — например, 20% прибыли и 5% допустимых потерь, а с учетом поведения конкретных акций и текущей ситуации на рынке. В течение трейда уровень «стопов» не должен быть фиксирован — по мере изменения цены акций он должен перемещаться. Планируемую прибыль иногда тоже можно и нужно менять. Рынок требует от трейдера большой гибкости, тем не менее, перед началом каждого трейда нужно четко представлять, что вы хотите получить от данных акций и что будете делать, если ваши предположения не оправдаются. Вот на этом этапе планирования и могут пригодиться идеи, описанные в данной главе.

Приведенные примеры, возможно, вселили в вас оптимизм и смутное чувство, что деньги на бирже делаются легко: надо только ставить «стопы» и дожидаться хорошей прибыли в случае удачного выбора акций. Если бы все было так просто, кто бы проигрывал?! Мы не будем приводить результаты более полного анализа реальных ситуаций, а только скажем, что прибыль, которая получается с использованием слепой стратегии (к примеру, X % прибыли и Y % допустимых потерь), очень небольшая. Из завершающейся главы вы, например, можете сделать вывод, что наилучшей стратегией является расстановка близких «стопов» и ожидание больших прибылей. Однако перед покупкой акций необходимо взвесить реальность получения высокой прибыли для данных акций. Безусловно такие акции есть, но ожидать в короткое время высокой прибыли порядка 30 — 50 % от всех акций было бы наивно и разорительно. В дальнейшем мы рассмотрим, как можно оценивать наиболее вероятную прибыль для конкретных акций. И еще всегда нужно учитывать, — особенно если вы играете небольшой суммой, — что потери на комиссионных, на разнице между покупной и продажной ценой и на других накладных расходах (платные источники информации, телефонные разговоры и т.п.) могут «съесть» ваши прибыли. Методы, описанные в данном разделе, лучше рассматривать не как рецепты получения сверхприбылей, а как способы страховки от разорительных потерь. Для хороших прибылей, существенно превышающих среднее изменение цен акций на рынке, необходимо постоянно искать перспективные акции, у которых вероятность роста устойчиво превышает вероятность падения. Тут важен каждый процент, и вам нужно научиться определять вероятность роста акций.